振幅放大¶

振幅放大（Amplitude Amplification）线路的主要作用为对于给定纯态的振幅进行放大，从而调整其测量结果概率分布。

算法背景¶

对于某个已知大小的可二元分类且标准 \(f\) 确定的有限集合 \(\Omega\)，基于 \(f\) 可以将集合中的任一元素\(\left|\psi\right\rangle\) 表示为两个正交基态 \(\left|\varphi_0\right\rangle,\left|\varphi_1\right\rangle\) 的线性组合。

\[\begin{aligned} \left|\psi\right\rangle=sin\theta\left|\varphi_1\right\rangle+cos\theta\left|\varphi_0\right\rangle, \ \left|\varphi_0\right\rangle=\left|\varphi_1^\bot\right\rangle. \end{aligned}\]

振幅放大量子线路可以将叠加态 \(\left|\psi\right\rangle\) 的表达式中 \(\left|\varphi_1\right\rangle\) 的振幅放大，从而得到一个结果量子态，能够以大概率测量得到目标量子态 \(\left|\varphi_1\right\rangle\)。

假设我们可以构造出某种量子门操作的组合，记该组合为振幅放大算子 \(Q\) ，将 \(Q\) 作用 \(k\) 次于量子态\(\left|\psi\right\rangle\) 上得到形如下式的量子态

\[\begin{aligned} \left|\psi_k\right\rangle=\sin{k\theta}\left|\varphi_1\right\rangle+\cos{k\theta} \ \left|\varphi_0\right\rangle,\ k\theta\approx\frac{\pi}{2}. \end{aligned}\]

那么就完成了所需的振幅放大量子线路构建。

相应的量子线路图如下：

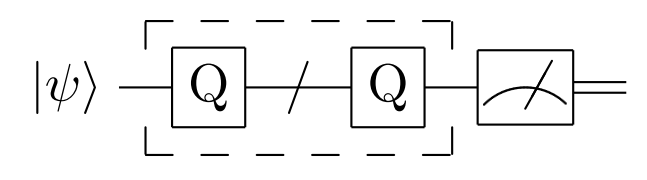
假设基于集合 \(\Omega\) 和分类标准 \(f\) 的量子态 \(\left|\psi\right\rangle\)已经完成制备，关键在于构造振幅放大算子 \(Q\) 。

定义振幅放大算子如下

\[\begin{aligned} P_1=I-2\left|\varphi_1\right\rangle \left\langle\varphi_1\right|, P=I-2\left|\psi\right\rangle \left\langle\psi\right|, Q=-PP_1. \end{aligned}\]

备注

如何通过集合 \(\Omega\) 和分类标准 \(f\) 来制备量子态？ \(P_1,P\) 又是怎样通过量子线路实现的？

简单验证可知在 \(\{\left|\varphi_1\right\rangle,\left|\varphi_0\right\rangle\}\)张成的空间中算子 \(Q\) 可以表示为

\[\begin{split}\begin{aligned} Q=\left[\begin{matrix}\cos{\left(2\theta\right)}&-\sin{\left(2\theta\right)}\\ \sin{\left(2\theta\right)}&\cos{\left(2\theta\right)}\\\end{matrix}\right] \end{aligned}\end{split}\]

实质上可以视为一个角度为 \(2\theta\) 的旋转量子门操作。因此有

\[\begin{aligned} Q^n\left|\psi\right\rangle=\sin{\left(2n+1\right)\theta}\left|\varphi_1 \right\rangle+\cos{\left(2n+1\right)\theta}\left|\varphi_0\right\rangle. \end{aligned}\]

选取合适的旋转次数 \(n\) 使得 \(\sin^2{\left(2n+1\right)\theta}\) 最接近 \(1\) 即可完成振幅放大量子线路。

相比经典的遍历分类方法，振幅放大量子线路可以充分体现量子计算的优势。

代码实例¶

取 \(\Omega=\{0,1\}, \left|\psi\right\rangle = \sin{\frac{\pi}{6}}\left|1\right\rangle+ \cos{\frac{\pi}{6}}\left|0\right\rangle,\ P_1=I-2\left|1\right\rangle \left\langle 1\right|=Z, P=I-2\left|\psi\right\rangle \left\langle\psi\right|\)，

振幅放大量子线路的相应代码实例如下

#include "QPanda.h"
using namespace QPanda;

int main(void)
{
   auto qvm = CPUQVM();
   qvm.init();
   // 申请寄存器并初始化
   QVec qvec = qvm.qAllocMany(1);

   // 构建振幅放大量子线路
   auto prog = QProg();
   prog << RY(qvec[0], PI / 3);
   prog << Z(qvec[0]) << RY(qvec[0], PI * 4 / 3);

   // 以概率方法输出结果量子态的理论值（并非测量）
   auto result = qvm.probRunDict(prog, qvec);
   qvm.finalize();

   // 输出结果
   for (auto& aiter : result)
   {
      cout << aiter.first << " : " << aiter.second << endl;
   }

   return 0;
}

输出结果应如下所示，分别以 \(1\) 和 \(0\) 的概率得到 \(\left|1\right\rangle\)和 \(\left|0\right\rangle\) ：

0:0
1:1