张量网络量子虚拟机¶
对于一个 \(N\) 个量子比特的自旋体系,对应的希尔伯特空间维数为 \(2^{N}\) 。
对于该复杂系统的状态演化,传统的全振幅模拟器将其看做一个有 \(2^{N}\) 个元素的一维向量。
然而从张量网络的角度来看,整个系统量子态的系数对应 \(2^{N}\) 维张量(即N阶张量,即有 \(N\) 个指标,每个指标的维数是2),量子操作算符的系数为 \(2^{2N}\) 维张量( \(2N\) 阶张量,即有个 \(2N\) 指标,每个指标的维数是2),我们可以用如下图形来表示量子态:
当量子系统的自旋个数增加时,量子态系数的个数随指数增加,称为指数墙问题,这一障碍限制了传统全振幅模拟器的最大模拟自旋数和模拟性能。
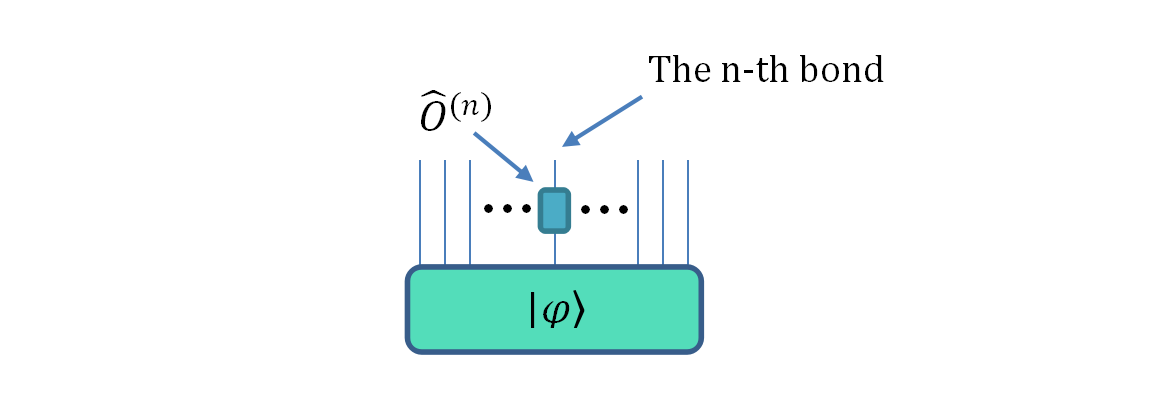
但是可通过张量网络处理这一问题,从而绕过指数墙障碍,在张量网络中,我们对量子系统的模拟,包括量子逻辑门操作和测量操作,均可以通过对于张量的缩并与分解来实现。矩阵乘积态是张量网络中最常用的表示形式,在多线性代数中称为张量列或TT(Tensor-Train),示意图如下。

将量子态分解成等式右边的表示形式,对于量子线路中部分量子逻辑门操作,可以将全局问题转化为局部的张量处理问题,从而有效地降低了时间复杂度和空间复杂度。
应用场景¶
在量子电路的模拟方法中,选择合适的模拟后端非常重要,不同量子线路模拟器的适用场所如下:
全振幅量子虚拟机:全振幅模拟器可以同时模拟和存储量子态的全部振幅,但受限于机器的内存条件,量子比特达到50位已是极限,适合低比特高深度的量子线路,比如低比特下的谷歌随机量子线路以及需要获取全部模拟结果的场景等。
部分振幅量子虚拟机:部分振幅模拟器依赖于其他模拟器提供的低比特量子线路振幅模拟结果,能模拟更高的比特数量,但能模拟的深度降低,通常用于获取量子态振幅的部分子集模拟结果。
单振幅量子虚拟机:单振幅模拟器能模拟更高的量子比特线路图,同时模拟的性能较高,不会随着量子比特数目增加呈指数型增长,但随着线路深度增加,模拟性能急剧下降,同时难以模拟多控制门也是其缺点,该模拟器适用于高比特低深度的量子线路模拟,通常用于快速地模拟获得单个量子态振幅结果。
张量网络量子虚拟机:张量网络模拟器与单振幅类似,与单振幅对比,可以模拟多控制门,同时在深度较高的线路模拟上存在性能优势。
量子云虚拟机:量子云虚拟机可以将任务提交在远程高性能计算集群上运行,突破本地硬件性能限制,同时支持在真实的量子芯片上运行量子算法。
使用介绍¶
QPanda2 中设计了 MPSQVM 类用于使用这一方法的模拟器进行模拟量子电路。和许多其他模拟器的使用方法一样,都具有相同的量子虚拟机接口,比如下述代码:
#include "QPanda.h" USING_QPANDA int main(void) { //首先构建一个张量网络模拟器 MPSQVM qvm; //对模拟比特上限进行配置 Configuration config = { 64,64 }; qvm.setConfig(config); //初始化和配置量子虚拟机环境 qvm.init(); auto qlist = qvm.qAllocMany(30); auto clist = qvm.cAllocMany(30); //构建量子算法对应的量子线路 QProg prog; prog << HadamardQCircuit(qlist) << CNOT(qlist[1], qlist[5]) << CZ(qlist[3], qlist[5]) << MeasureAll(qlist,clist); //调用模拟接口,获取模拟结果 auto result = qvm.runWithConfiguration(prog, clist, 1000); //释放量子虚拟机系统资源 qvm.finalize(); }
完整示例代码¶
以下示例展示了张量网络模拟器计算部分接口的使用方式
#include "QPanda.h" USING_QPANDA int main(void) { MPSQVM qvm; qvm.init(); auto qlist = qvm.qAllocMany(10); auto clist = qvm.cAllocMany(10); QProg prog; prog << HadamardQCircuit(qlist) << CZ(qlist[1], qlist[5]) << CZ(qlist[3], qlist[5]) << CZ(qlist[2], qlist[4]) << CZ(qlist[3], qlist[7]) << CZ(qlist[0], qlist[4]) << RY(qlist[7], PI / 2) << RX(qlist[8], PI / 2) << RX(qlist[9], PI / 2) << CR(qlist[0], qlist[1], PI) << CR(qlist[2], qlist[3], PI) << RY(qlist[4], PI / 2) << RZ(qlist[5], PI / 4) << RX(qlist[6], PI / 2) << RZ(qlist[7], PI / 4) << CR(qlist[8], qlist[9], PI) << CR(qlist[1], qlist[2], PI) << RY(qlist[3], PI / 2) << RX(qlist[4], PI / 2) << RX(qlist[5], PI / 2) << CR(qlist[9], qlist[1], PI) << RY(qlist[1], PI / 2) << RY(qlist[2], PI / 2) << RZ(qlist[3], PI / 4) << CR(qlist[7], qlist[8], PI) <<MeasureAll(qlist,clist); auto measure_result = qvm.runWithConfiguration(prog, clist, 1000); for (auto val : measure_result) { cout << val.first << " : " << val.second << endl; } auto pmeasure_result = qvm.probRunDict(prog, qlist, -1); for (auto val : pmeasure_result) { cout << val.first << " : " << val.second << endl; } qvm.finalize(); return 0; }
runWithConfiguration与probRunDict接口分别用于Monte Carlo采样模拟和概率测量,他们分别输出模拟采样的结果和对应振幅的概率,上述程序的计算结果如下//Monte Carlo 采样模拟结果 0000000111 : 1 0000110110 : 1 0000111000 : 2 0001000001 : 3 0001000100 : 1 0001001101 : 1 0001010000 : 2 0001101100 : 1 0001110110 : 1 ... //概率测量结果 0000000000 : 0.0016671 0000000001 : 0.0016671 0000000010 : 0.000286029 0000000011 : 0.000286029 0000000100 : 0.000286029 0000000101 : 0.000286029 0000000110 : 0.0016671 0000000111 : 0.0016671 0000001000 : 0.0016671 0000001001 : 0.0016671 0000001010 : 0.000286029 0000001011 : 0.000286029 ...备注
概率测量还支持其他输出类型的接口,比如
getProbTupleList(QVec, int)、probRunTupleList(QProg &, QVec, int)、probRunList(QProg &, QVec, int)、getQState()以及pMeasure(QVec, int)等,在此不做过多介绍。后续张量网络量子虚拟机会支持含噪声的模拟,使量子电路的模拟更贴近真实的量子计算机,支持自定义的逻辑门类型和噪声模型,所有的噪声模型和错误包括但不限于 含噪声量子虚拟机 部分提到的内容。