优化算法(直接搜索法)¶
本章节将讲解优化算法的使用,包括 Nelder-Mead 算法跟 Powell 算法,它们都是一种直接搜索算法。我们在 QPanda 中实现了这两个算法,OriginNelderMead 和 OriginPowell ,
这两个类都继承自 AbstractOptimizer 。
接口介绍¶
我们可以通过优化器工厂生成指定类型的优化器,例如我们指定它的类型为Nelder-Mead
using namespace QPanda;
auto optimizer = OptimizerFactory::makeOptimizer(NELDER_MEAD);
我们需要向优化器注册一个计算损失值的函数和待优化参数。
vector_d init_para{0, 0};
optimizer->registerFunc(myFunc, init_para);
然后设置结束条件,我们可以设置变量及函数值的收敛阈值,函数最大可调用次数,和优化迭代次数。只要满足上述结束条件,则优化结束。
optimizer->setXatol(1e-6);
optimizer->setFatol(1e-6);
optimizer->setMaxFCalls(200);
optimizer->setMaxIter(200);
然后通过exec接口执行优化,通过getResult接口获得优化后的结果。
optimizer->exec();
auto result = optimizer->getResult();
实例¶
给定一些散列点,我们来拟合一条直线,使得散列点到直线的距离和最小。定义直线的函数的表达式为 y = w*x + b ,接下来我们将通过使用优化算法得到w和b的优化值。 首先定义求期望的函数
QPanda::QResultPair myFunc(QPanda::vector_d para, QPanda::vector_d &grad, int iter, int fcall)
{
std::vector<double> x = {3.3, 4.4, 5.5, 6.71, 6.93, 4.168, 9.779, 6.182, 7.59,
2.167, 7.042, 10.791, 5.313, 7.997, 5.654, 9.27, 3.1};
std::vector<double> y = {1.7, 2.76, 2.09, 3.19, 1.694, 1.573, 3.366, 2.596, 2.53,
1.221, 2.827, 3.465, 1.65, 2.904, 2.42, 2.94, 1.3};
std::vector<double> y_;
for (auto i = 0u; i < x.size(); i++)
{
y_.push_back(para[0]*x[i] + para[1]);
}
float loss = 0;
for (auto i = 0u; i < y.size(); i++)
{
loss += std::pow(y[i] - y_[i], 2)/y.size();
}
return std::make_pair("", loss);
}
我们使用 Nelder-Mead 算法进行优化
#include "Components/Optimizer/AbstractOptimizer.h"
#include "Components/Optimizer/OptimizerFactory.h"
#include <iostream>
int main()
{
auto optimizer = QPanda::OptimizerFactory::makeOptimizer(QPanda::OptimizerType::NELDER_MEAD);
QPanda::vector_d init_para{0, 0};
optimizer->registerFunc(myFunc, init_para);
optimizer->setXatol(1e-6);
optimizer->setFatol(1e-6);
optimizer->setMaxFCalls(200);
optimizer->setMaxIter(200);
optimizer->exec();
auto result = optimizer->getResult();
std::cout << result.message << std::endl;
std::cout << " Current function value: "
<< result.fun_val << std::endl;
std::cout << " Iterations: "
<< result.iters << std::endl;
std::cout << " Function evaluations: "
<< result.fcalls << std::endl;
std::cout << " Optimized para: " << std::endl;
for (auto i = 0u; i < result.para.size(); i++)
{
std::cout << " " << result.para[i] << std::endl;
}
}

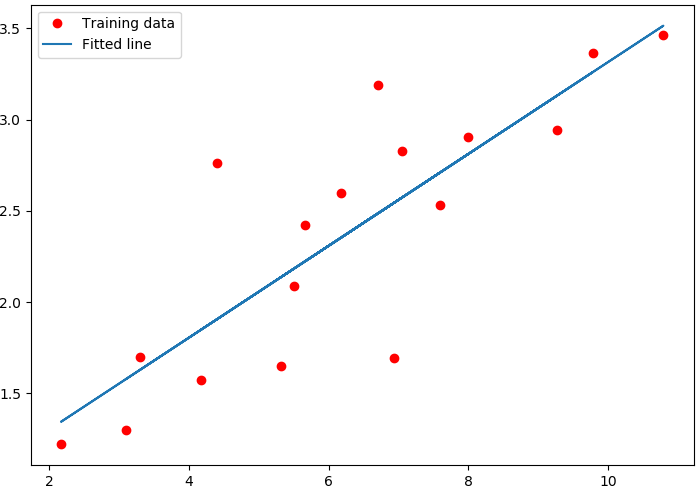
我们将散列点和拟合的直线进行绘图