Classical Neural Network Module

The following classical neural network modules support automatic back propagation computation.After running the forward function, you can calculate the gradient by executing the reverse function.A simple example of the convolution layer is as follows:

from pyvqnet.tensor import arange
from pyvqnet import kfloat32
from pyvqnet.nn import Conv2D

# an image feed into two dimension convolution layer
b = 2        # batch size
ic = 2       # input channels
oc = 2      # output channels
hw = 4      # input width and heights

# two dimension convolution layer
test_conv = Conv2D(ic,oc,(2,2),(2,2),"same")

# input of shape [b,ic,hw,hw]
x0 = arange(1,b*ic*hw*hw+1,requires_grad=True,dtype=kfloat32)

x1 = x0.reshape([b,ic,hw,hw])
#forward function
x = test_conv(x1)

#backward function with autograd
x.backward()
print(x0.grad)

# [
# [[[0.0958736, 0.3032238, 0.0958736, 0.3032238],
#  [-0.2665333, 0.1081382, -0.2665333, 0.1081382],
#  [0.0958736, 0.3032238, 0.0958736, 0.3032238],
#  [-0.2665333, 0.1081382, -0.2665333, 0.1081382]],
# [[-0.0068994, 0.0914679, -0.0068994, 0.0914679],
#  [-0.2820665, 0.3160213, -0.2820665, 0.3160213],
#  [-0.0068994, 0.0914679, -0.0068994, 0.0914679],
#  [-0.2820665, 0.3160213, -0.2820665, 0.3160213]]],
# [[[0.0958736, 0.3032238, 0.0958736, 0.3032238],
#  [-0.2665333, 0.1081382, -0.2665333, 0.1081382],
#  [0.0958736, 0.3032238, 0.0958736, 0.3032238],
#  [-0.2665333, 0.1081382, -0.2665333, 0.1081382]],
# [[-0.0068994, 0.0914679, -0.0068994, 0.0914679],
#  [-0.2820665, 0.3160213, -0.2820665, 0.3160213],
#  [-0.0068994, 0.0914679, -0.0068994, 0.0914679],
#  [-0.2820665, 0.3160213, -0.2820665, 0.3160213]]]
# ]

Module Class

abstract calculation module

Module

class pyvqnet.nn.module.Module

Base class for all neural network modules including quantum modules or classic modules. Your models should also be subclass of this class for autograd calculation.

Modules can also contain other Modules, allowing to nest them in a tree structure. You can assign the submodules as regular attributes:

class Model(Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = pyvqnet.nn.Conv2d(1, 20, (5,5))
        self.conv2 = pyvqnet.nn.Conv2d(20, 20, (5,5))

    def forward(self, x):
        x = pyvqnet.nn.activation.relu(self.conv1(x))
        return pyvqnet.nn.activation.relu(self.conv2(x))

Submodules assigned in this way will be registered

forward

pyvqnet.nn.module.Module.forward(x, *args, **kwargs)

Abstract method which performs forward pass.

参数:

• x – input QTensor

• *args – A non-keyword variable parameter

• **kwargs – A keyword variable parameter

返回:

module output

Example:

import numpy as np
from pyvqnet.tensor import QTensor
import pyvqnet as vq
from pyvqnet.nn import Conv2D
b = 2
ic = 3
oc = 2
test_conv = Conv2D(ic, oc, (3, 3), (2, 2), "same")
x0 = QTensor(np.arange(1, b * ic * 5 * 5 + 1).reshape([b, ic, 5, 5]),
            requires_grad=True,
            dtype=vq.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[[4.3995643, 3.9317808, -2.0707254],
#  [20.1951981, 21.6946659, 14.2591858],
#  [38.4702759, 31.9730244, 24.5977650]],
# [[-17.0607567, -31.5377998, -7.5618000],
#  [-22.5664024, -40.3876266, -15.1564388],
#  [-3.1080279, -18.5986233, -8.0648050]]],
# [[[6.6493244, -13.4840755, -20.2554188],
#  [54.4235802, 34.4462433, 26.8171902],
#  [90.2827682, 62.9092331, 51.6892929]],
# [[-22.3385429, -45.2448578, 5.7101378],
#  [-32.9464149, -60.9557228, -10.4994345],
#  [5.9029331, -20.5480480, -0.9379558]]]
# ]

state_dict

pyvqnet.nn.module.Module.state_dict(destination=None, prefix='')

Return a dictionary containing a whole state of the module.

Both parameters and persistent buffers (e.g. running averages) are included. Keys are corresponding parameter and buffer names.

参数:

• destination – a dict where state will be stored

• prefix – the prefix for parameters and buffers used in this module

返回:

a dictionary containing a whole state of the module

Example:

from pyvqnet.nn import Conv2D
test_conv = Conv2D(2,3,(3,3),(2,2),"same")
print(test_conv.state_dict().keys())
#odict_keys(['weights', 'bias'])

toGPU

pyvqnet.nn.module.Module.toGPU(device: int = DEV_GPU_0)

Move the parameters and buffer data of a module and its submodules to the specified GPU device.

device specifies the device whose internal data is stored. When device >= DEV_GPU_0, the data is stored on the GPU. If your computer has multiple GPUs, You can specify different devices to store data. For example, device = DEV_GPU_1 , DEV_GPU_2, DEV_GPU_3, … means it is stored on GPUs with different serial numbers.

备注

Module cannot be calculated on different GPUs. A Cuda error will be raised if you try to create a QTensor on a GPU whose ID exceeds the maximum number of verified GPUs.

参数:

device – The device currently saving QTensor, default=DEV_GPU_0. device = pyvqnet.DEV_GPU_0, stored in the first GPU, devcie = DEV_GPU_1, stored in the second GPU, and so on.

返回:

Module moved to GPU device.

Examples:

from pyvqnet.nn.conv import ConvT2D
test_conv = ConvT2D(3, 2, [4,4], [2, 2], "same")
test_conv = test_conv.toGPU()
print(test_conv.backend)
#1000

toCPU

pyvqnet.nn.module.Module.toCPU()

Moves the parameters and buffer data of a module and its submodules to a specific CPU device.

返回:

Module moved to CPU device.

Examples:

from pyvqnet.nn.conv import ConvT2D
test_conv = ConvT2D(3, 2, [4,4], [2, 2], "same")
test_conv = test_conv.toCPU()
print(test_conv.backend)
#0

save_parameters

pyvqnet.utils.storage.save_parameters(obj, f)

Saves model parmeters to a disk file.

参数:

• obj – saved OrderedDict from state_dict()

• f – a string or os.PathLike object containing a file name

返回:

None

Example:

from pyvqnet.nn import Module,Conv2D
import pyvqnet
class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = Conv2D(input_channels=1, output_channels=6, kernel_size=(5, 5), stride=(1, 1), padding="valid")

    def forward(self, x):
        return super().forward(x)

model = Net()
pyvqnet.utils.storage.save_parameters(model.state_dict(),"tmp.model")

load_parameters

pyvqnet.utils.storage.load_parameters(f)

Loads model paramters from a disk file.

The model instance should be created first.

参数:

f – a string or os.PathLike object containing a file name

返回:

saved OrderedDict for load_state_dict()

Example:

from pyvqnet.nn import Module,Conv2D
import pyvqnet

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = Conv2D(input_channels=1, output_channels=6, kernel_size=(5, 5), stride=(1, 1), padding="valid")

    def forward(self, x):
        return super().forward(x)

model = Net()
model1 = Net()  # another Module object
pyvqnet.utils.storage.save_parameters( model.state_dict(),"tmp.model")
model_para =  pyvqnet.utils.storage.load_parameters("tmp.model")
model1.load_state_dict(model_para)

ModuleList

class pyvqnet.nn.module.ModuleList([pyvqnet.nn.module.Module])

Save submodules in a list. ModuleList can be indexed like a normal Python list, and the internal parameters of the Module it contains can be saved.

参数:

modules – list of nn.Modules

返回:

a list of modules

Example:

from pyvqnet.tensor import *
from pyvqnet.nn import Module,Linear,ModuleList
from pyvqnet.qnn import ProbsMeasure,QuantumLayer
import pyqpanda as pq
def pqctest (input,param,qubits,cubits,m_machine):
    circuit = pq.QCircuit()
    circuit.insert(pq.H(qubits[0]))
    circuit.insert(pq.H(qubits[1]))
    circuit.insert(pq.H(qubits[2]))
    circuit.insert(pq.H(qubits[3]))

    circuit.insert(pq.RZ(qubits[0],input[0]))
    circuit.insert(pq.RZ(qubits[1],input[1]))
    circuit.insert(pq.RZ(qubits[2],input[2]))
    circuit.insert(pq.RZ(qubits[3],input[3]))

    circuit.insert(pq.CNOT(qubits[0],qubits[1]))
    circuit.insert(pq.RZ(qubits[1],param[0]))
    circuit.insert(pq.CNOT(qubits[0],qubits[1]))

    circuit.insert(pq.CNOT(qubits[1],qubits[2]))
    circuit.insert(pq.RZ(qubits[2],param[1]))
    circuit.insert(pq.CNOT(qubits[1],qubits[2]))

    circuit.insert(pq.CNOT(qubits[2],qubits[3]))
    circuit.insert(pq.RZ(qubits[3],param[2]))
    circuit.insert(pq.CNOT(qubits[2],qubits[3]))


    prog = pq.QProg()
    prog.insert(circuit)

    rlt_prob = ProbsMeasure([0,2],prog,m_machine,qubits)
    return rlt_prob


class M(Module):
    def __init__(self):
        super(M, self).__init__()
        self.pqc2 = ModuleList([QuantumLayer(pqctest,3,"cpu",4,1), Linear(4,1)
        ])

    def forward(self, x, *args, **kwargs):
        y = self.pqc2[0](x)  + self.pqc2[1](x)
        return y

mm = M()
print(mm.state_dict().keys())
#odict_keys(['pqc2.0.m_para', 'pqc2.1.weights', 'pqc2.1.bias'])

ParameterList

class pyvqnet.nn.module.ParameterList([pyvqnet.nn.module.Module])

To store parameters in a list, a ParameterList can be indexed like a normal Python list, and the internal parameters of the Parameter it contains can be stored.

参数:

modules – nn.Parameter list.

返回:

a Parameter list.

Example:

from pyvqnet import nn
class MyModule(nn.Module):
    def __init__(self):
        super().__init__()
        self.params = nn.ParameterList([nn.Parameter((10, 10)) for i in range(10)])
    def forward(self, x):

        # ParameterList can act as an iterable, or be indexed using ints
        for i, p in enumerate(self.params):
            x = self.params[i // 2] * x + p * x
        return x

model = MyModule()
print(model.state_dict().keys())

Sequential

class pyvqnet.nn.module.Sequential([pyvqnet.nn.module.Module])

Modules will be added in the order they are passed in. Alternatively, a OrderedDict of modules can be passed in. The forward() method of Sequential takes any input and forwards it to its first module. It then Sequential the output to the input of each subsequent module in turn, and finally returns the output of the last module.

参数:

modules – module to append.

返回:

Sequential.

Example:

from pyvqnet import nn
from collections import OrderedDict

# Using Sequential to create a small model.
model = nn.Sequential(
          nn.Conv2D(1,20,(5, 5)),
          nn.ReLu(),
          nn.Conv2D(20,64,(5, 5)),
          nn.ReLu()
        )
print(model.state_dict().keys())

# Using Sequential with OrderedDict. This is functionally the same as the above code

model = nn.Sequential(OrderedDict([
          ('conv1', nn.Conv2D(1,20,(5, 5))),
          ('relu1', nn.ReLu()),
          ('conv2', nn.Conv2D(20,64,(5, 5))),
          ('relu2', nn.ReLu())
        ]))
print(model.state_dict().keys())

Classical Neural Network Layer

Conv1D

class pyvqnet.nn.Conv1D(input_channels: int, output_channels: int, kernel_size: int, stride: int = 1, padding='valid', use_bias: str = True, kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, group: int = 1, dtype=None, name='')

Apply a 1-dimensional convolution kernel over an input . Inputs to the conv module are of shape (batch_size, input_channels, height)

参数:

• input_channels – int - Number of input channels

• output_channels – int - Number of kernels

• kernel_size – int - Size of a single kernel. kernel shape = [output_channels,input_channels/group,kernel_size,1]

• stride – int - Stride, defaults to 1

• padding – str|int - padding option, which can be a string {‘valid’, ‘same’} or an integer giving the amount of implicit padding to apply . Default “valid”.

• use_bias – bool - if use bias, defaults to True

• kernel_initializer – callable - Defaults to None

• bias_initializer – callable - Defaults to None

• dilation_rate – int - dilated size, defaults: 1

• group – int - number of groups of grouped convolutions. Default: 1

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – The name of the module, default: “”.

返回:

a Conv1D class

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Conv1D
import pyvqnet
b= 2
ic =3
oc = 2
test_conv = Conv1D(ic,oc,3,2,"same")
x0 = QTensor(np.arange(1,b*ic*5*5 +1).reshape([b,ic,25]),requires_grad=True,dtype=pyvqnet.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[12.4438553, 14.8618164, 15.5595102, 16.2572021, 16.9548950, 17.6525879, 18.3502808, 19.0479736, 19.7456665, 20.4433594, 21.1410522, 21.8387432, 10.5725441],
#  [-13.7539215, 1.0263026, 1.2747254, 1.5231485, 1.7715728, 2.0199962, 2.2684195, 2.5168428, 2.7652662, 3.0136888, 3.2621140, 3.5105357, 14.0515862]],
# [[47.4924164, 41.0252953, 41.7229881, 42.4206772, 43.1183739, 43.8160667, 44.5137596, 45.2114487, 45.9091415, 46.6068344, 47.3045311, 48.0022240, 18.3216572],
#  [-47.2381554, 10.3421783, 10.5906038, 10.8390274, 11.0874519, 11.3358765, 11.5842953, 11.8327246, 12.0811434, 12.3295631, 12.5779924, 12.8264122, 39.4719162]]
# ]

Conv2D

class pyvqnet.nn.Conv2D(input_channels: int, output_channels: int, kernel_size: tuple, stride: tuple = (1, 1), padding='valid', use_bias=True, kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, group: int = 1, dtype=None, name='')

Apply a two-dimensional convolution kernel over an input . Inputs to the conv module are of shape (batch_size, input_channels, height, width)

参数:

• input_channels – int - Number of input channels

• output_channels – int - Number of kernels

• kernel_size – tuple|list - Size of a single kernel. kernel shape = [output_channels,input_channels/group,kernel_size,kernel_size]

• stride – tuple|list - Stride, defaults to (1, 1)|[1,1]

• padding – str|tuple - padding option, which can be a string {‘valid’, ‘same’} or a tuple of integers giving the amount of implicit padding to apply on both sides. Default “valid”.

• use_bias – bool - if use bias, defaults to True

• kernel_initializer – callable - Defaults to None

• bias_initializer – callable - Defaults to None

• dilation_rate – int - dilated size, defaults: 1

• group – int - number of groups of grouped convolutions. Default: 1.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – The name of the module, default: “”.

返回:

a Conv2D class

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Conv2D
import pyvqnet
b= 2
ic =3
oc = 2
test_conv = Conv2D(ic,oc,(3,3),(2,2),"same")
x0 = QTensor(np.arange(1,b*ic*5*5+1).reshape([b,ic,5,5]),requires_grad=True,dtype=pyvqnet.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[[-0.1256833, 23.8978596, 26.7449780],
#  [-7.2959919, 33.4023743, 42.1283913],
#  [-8.7684336, 25.2698975, 40.4024887]],
# [[33.0653763, 40.3120155, 27.3781891],
#  [39.2921371, 45.8685760, 38.1885109],
#  [23.1873779, 12.0480318, 12.7278290]]],
# [[[-0.9730744, 61.3967094, 79.0511856],
#  [-29.3652401, 75.0349350, 112.7325439],
#  [-26.4682808, 59.0924797, 104.2572098]],
# [[66.8064194, 96.0953140, 72.9157486],
#  [90.9154129, 110.7232437, 91.2616043],
#  [56.8825951, 34.6904907, 30.1957760]]]
# ]

ConvT2D

class pyvqnet.nn.ConvT2D(input_channels, output_channels, kernel_size, stride=[1, 1], padding='valid', use_bias='True', kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, out_padding=(0, 0), group: int = 1, dtype=None, name='')

Apply a two-dimensional transposed convolution kernel over an input. Inputs to the convT module are of shape (batch_size, input_channels, height, width)

参数:

• input_channels – int - Number of input channels

• output_channels – int - Number of kernels

• kernel_size – tuple|list - Size of a single kernel. kernel shape = [input_channels,output_channels/group,kernel_size,kernel_size]

• stride – tuple|list - Stride, defaults to (1, 1)|[1,1]

• padding – str|tuple - padding option, which can be a string {‘valid’, ‘same’} or a tuple of integers giving the amount of implicit padding to apply on both sides. Default “valid”.

• use_bias – bool - Whether to use a offset item. Default to use

• kernel_initializer – callable - Defaults to None

• bias_initializer – callable - Defaults to None

• dilation_rate – int - dilated size, defaults: 1.

• out_padding – Additional size added to one side of each dimension in the output shape. Default: (0,0)

• group – int - number of groups of grouped convolutions. Default: 1.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – The name of the module, default: “”.

返回:

a ConvT2D class

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import ConvT2D
import pyvqnet
test_conv = ConvT2D(3, 2, (3, 3), (1, 1), "valid")
x = QTensor(np.arange(1, 1 * 3 * 5 * 5+1).reshape([1, 3, 5, 5]), requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-3.3675897, 4.8476148, 14.2448473, 14.8897810, 15.5347166, 20.0420666, 10.9831696],
#  [-14.0110836, -3.2500827, 6.4022207, 6.5149083, 6.6275964, 23.7946320, 12.1828709],
#  [-22.2661152, -3.5112300, 12.9493723, 13.5486069, 14.1478367, 39.6327629, 18.8349991],
#  [-24.4063797, -3.0093837, 15.9455290, 16.5447617, 17.1439915, 44.7691879, 21.3293095],
#  [-26.5466480, -2.5075383, 18.9416828, 19.5409145, 20.1401463, 49.9056053, 23.8236179],
#  [-24.7624626, -13.7395811, -7.9510674, -7.9967723, -8.0424776, 19.2783546, 7.0562835],
#  [-3.5170188, 10.2280807, 16.1939259, 16.6804695, 17.1670132, 21.2262039, 6.2889833]],
# [[-2.0570512, -9.5056667, -25.0429192, -25.9464111, -26.8499031, -24.7305946, -16.9881954],
#  [-0.7620960, -18.3383904, -49.8948288, -51.2528229, -52.6108208, -52.2179604, -34.3664169],
#  [-11.7121849, -27.1864738, -62.2154846, -63.6433640, -65.0712280, -52.6787071, -38.4497032],
#  [-13.3643141, -29.0211792, -69.3548126, -70.7826691, -72.2105408, -58.1659012, -43.7543182],
#  [-15.0164423, -30.8558884, -76.4941254, -77.9219971, -79.3498535, -63.6530838, -49.0589256],
#  [-11.6070204, -14.1940546, -35.5471687, -36.0715408, -36.5959129, -23.9147663, -22.8668022],
#  [-14.4390459, -4.9011412, -6.4719801, -6.5418491, -6.6117167, 9.3329525, -1.7254852]]]
# ]

AvgPool1D

class pyvqnet.nn.AvgPool1D(kernel, stride, padding='valid', name='')

This operation applies a 1D average pooling over an input signal composed of several input planes.

参数:

• kernel – size of the average pooling windows

• strides – factor by which to downscale

• padding – one of “valid”, “same” or integer specifies the padding value, defaults to “valid”

• name – name of the output layer.

返回:

AvgPool1D layer

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import AvgPool1D
test_mp = AvgPool1D([3],[2],"same")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
# [
# [[0.3333333, 1.6666666, 3],
#  [1.6666666, 2, 1.3333334],
#  [2.6666667, 2.6666667, 2.3333333],
#  [2.3333333, 4.3333335, 3.3333333],
#  [0.3333333, 1.6666666, 4]]
# ]

MaxPool1D

class pyvqnet.nn.MaxPool1D(kernel, stride, padding='valid', dtype=None, name='')

This operation applies a 1D max pooling over an input signal composed of several input planes.

参数:

• kernel – size of the max pooling windows

• strides – factor by which to downscale

• padding – one of “valid”, “same” or integer specifies the padding value, defaults to “valid”

• name – The name of the module, default: “”.

返回:

MaxPool1D layer

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import MaxPool1D
test_mp = MaxPool1D([3],[2],"same")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
#[[[1. 4. 5.]
#   [3. 3. 3.]
#   [4. 4. 4.]
#   [5. 6. 6.]
#   [1. 5. 7.]]]

AvgPool2D

class pyvqnet.nn.AvgPool2D(kernel, stride, padding='valid', name='')

This operation applies 2D average pooling over input features .

参数:

• kernel – size of the average pooling windows

• strides – factors by which to downscale

• padding – one of “valid”, “same” or tuple with integers specifies the padding value of column and row,defaults to “valid”

• name – name of the output layer

返回:

AvgPool2D layer

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import AvgPool2D
test_mp = AvgPool2D([2,2],[2,2],"valid")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
#[[[[1.5  1.75]
#    [3.75 3.  ]]]]

MaxPool2D

class pyvqnet.nn.MaxPool2D(kernel, stride, padding='valid', name='')

This operation applies 2D max pooling over input features.

参数:

• kernel – size of the max pooling windows

• strides – factor by which to downscale

• padding – one of “valid”, “same” or tuple with integers specifies the padding value of column and row, defaults to “valid”

• name – name of the output layer

返回:

MaxPool2D layer

备注

padding='valid' is the same as no padding.

padding='same' pads the input so the output has the shape as the input.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import MaxPool2D
test_mp = MaxPool2D([2,2],[2,2],"valid")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
# [[[[3. 4.]
#    [5. 6.]]]]

Embedding

class pyvqnet.nn.embedding.Embedding(num_embeddings, embedding_dim, weight_initializer=<function xavier_normal>, dtype=None, name: str = '')

This module is often used to store word embeddings and retrieve them using indices. The input to the module is a list of indices, and the output is the corresponding word embeddings.

参数:

• num_embeddings – int - size of the dictionary of embeddings.

• embedding_dim – int - the size of each embedding vector.

• weight_initializer – callable - defaults to normal.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer.

返回:

a Embedding class

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn.embedding import Embedding
import pyvqnet
vlayer = Embedding(30,3)
x = QTensor(np.arange(1,25).reshape([2,3,2,2]),dtype= pyvqnet.kint64)
y = vlayer(x)
print(y)

# [
# [[[[-0.3168081, 0.0329394, -0.2934906],
#  [0.1057295, -0.2844988, -0.1687456]],
# [[-0.2382513, -0.3642318, -0.2257225],
#  [0.1563180, 0.1567665, 0.3038477]]],
# [[[-0.4131152, -0.0564500, -0.2804018],
#  [-0.2955172, -0.0009581, -0.1641144]],
# [[0.0692555, 0.1094901, 0.4099118],
#  [0.4348361, 0.0304361, -0.0061203]]],
# [[[-0.3310401, -0.1836129, 0.1098949],
#  [-0.1840732, 0.0332474, -0.0261806]],
# [[-0.1489778, 0.2519453, 0.3299376],
#  [-0.1942692, -0.1540277, -0.2335350]]]],
# [[[[-0.2620637, -0.3181309, -0.1857461],
#  [-0.0878164, -0.4180320, -0.1831555]],
# [[-0.0738970, -0.1888980, -0.3034399],
#  [0.1955448, -0.0409723, 0.3023460]]],
# [[[0.2430045, 0.0880465, 0.4309453],
#  [-0.1796514, -0.1432367, -0.1253638]],
# [[-0.5266719, 0.2386262, -0.0329155],
#  [0.1033449, -0.3442690, -0.0471130]]],
# [[[-0.5336705, -0.1939755, -0.3000667],
#  [0.0059001, 0.5567381, 0.1926173]],
# [[-0.2385869, -0.3910453, 0.2521235],
#  [-0.0246447, -0.0241158, -0.1402829]]]]
# ]

BatchNorm2d

class pyvqnet.nn.BatchNorm2d(channel_num: int, momentum: float = 0.1, epsilon: float = 1e-5, affine=True, beta_initializer=zeros, gamma_initializer=ones, dtype=None, name='')

Applies Batch Normalization over a 4D input (B,C,H,W) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

where \(\gamma\) and \(\beta\) are learnable parameters.Also by default, during training this layer keeps running estimates of its computed mean and variance, which are then used for normalization during evaluation. The running estimates are kept with a default momentum of 0.1.

参数:

• channel_num – int - the number of input features channels.

• momentum – float - momentum when calculation exponentially weighted average, defaults to 0.1.

• epsilon – float - numerical stability constant, defaults to 1e-5.

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• beta_initializer – callable - defaults to zeros.

• gamma_initializer – callable - defaults to ones.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

a BatchNorm2d class

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import BatchNorm2d
import pyvqnet
b = 2
ic = 2
test_conv = BatchNorm2d(ic)

x = QTensor(np.arange(1, 17).reshape([b, ic, 4, 1]),
            requires_grad=True,
            dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-1.3242440],
#  [-1.0834724],
#  [-0.8427007],
#  [-0.6019291]],
# [[-1.3242440],
#  [-1.0834724],
#  [-0.8427007],
#  [-0.6019291]]],
# [[[0.6019291],
#  [0.8427007],
#  [1.0834724],
#  [1.3242440]],
# [[0.6019291],
#  [0.8427007],
#  [1.0834724],
#  [1.3242440]]]
# ]

BatchNorm1d

class pyvqnet.nn.BatchNorm1d(channel_num: int, momentum: float = 0.1, epsilon: float = 1e-5, affine=True, beta_initializer=zeros, gamma_initializer=ones, dtype=None, name='')

Applies Batch Normalization over a 2D input (B,C) as described in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift .

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

where \(\gamma\) and \(\beta\) are learnable parameters.Also by default, during training this layer keeps running estimates of its computed mean and variance, which are then used for normalization during evaluation. The running estimates are kept with a default momentum of 0.1.

参数:

• channel_num – int - the number of input features channels.

• momentum – float - momentum when calculation exponentially weighted average, defaults to 0.1

• epsilon – float - numerical stability constant, defaults to 1e-5.

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• beta_initializer – callable - defaults to zeros.

• gamma_initializer – callable - defaults to ones.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

a BatchNorm1d class

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import BatchNorm1d
import pyvqnet
test_conv = BatchNorm1d(4)

x = QTensor(np.arange(1, 17).reshape([4, 4]),
            requires_grad=True,
            dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)


# [
# [-1.3416405, -1.3416405, -1.3416405, -1.3416405],
# [-0.4472135, -0.4472135, -0.4472135, -0.4472135],
# [0.4472135, 0.4472135, 0.4472135, 0.4472135],
# [1.3416405, 1.3416405, 1.3416405, 1.3416405]
# ]

LayerNormNd

class pyvqnet.nn.layer_norm.LayerNormNd(normalized_shape: list, epsilon: float = 1e-5, affine=True, dtype=None, name='')

Layer normalization is performed on the last several dimensions of any input. The specific method is as described in the paper: Layer Normalization。

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

For inputs like (B,C,H,W,D), norm_shape can be [C,H,W,D],[H,W,D],[W,D] or [D] .

参数:

• norm_shape – float - standardize the shape.

• epsilon – float - numerical stability constant, defaults to 1e-5.

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer.

返回:

a LayerNormNd class.

Example:

import numpy as np
from pyvqnet.tensor import QTensor
form pyvqnet import kfloat32
from pyvqnet.nn.layer_norm import LayerNormNd
ic = 4
test_conv = LayerNormNd([2,2])
x = QTensor(np.arange(1,17).reshape([2,2,2,2]),requires_grad=True,dtype=kfloat32)
y = test_conv.forward(x)
print(y)
# [
# [[[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]],
# [[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]]],
# [[[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]],
# [[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]]]
# ]

LayerNorm2d

class pyvqnet.nn.layer_norm.LayerNorm2d(norm_size: int, epsilon: float = 1e-5, affine=True, dtype=None, name='')

Applies Layer Normalization over a mini-batch of 4D inputs as described in the paper Layer Normalization

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

The mean and standard-deviation are calculated over the last D dimensions size.

For input like (B,C,H,W), norm_size should equals to C * H * W.

参数:

• norm_size – float - normalize size,equals to C * H * W

• epsilon – float - numerical stability constant, defaults to 1e-5

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• name – name of the output layer

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

返回:

a LayerNorm2d class

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn.layer_norm import LayerNorm2d
ic = 4
test_conv = LayerNorm2d(8)
x = QTensor(np.arange(1,17).reshape([2,2,4,1]),requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-1.5275238],
#  [-1.0910884],
#  [-0.6546531],
#  [-0.2182177]],
# [[0.2182177],
#  [0.6546531],
#  [1.0910884],
#  [1.5275238]]],
# [[[-1.5275238],
#  [-1.0910884],
#  [-0.6546531],
#  [-0.2182177]],
# [[0.2182177],
#  [0.6546531],
#  [1.0910884],
#  [1.5275238]]]
# ]

LayerNorm1d

class pyvqnet.nn.layer_norm.LayerNorm1d(norm_size: int, epsilon: float = 1e-5, affine=True, dtype=None, name='')

Applies Layer Normalization over a mini-batch of 2D inputs as described in the paper Layer Normalization

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

The mean and standard-deviation are calculated over the last dimensions size, where norm_size is the value of last dim size.

参数:

• norm_size – float - normalize size,equals to last dim

• epsilon – float - numerical stability constant, defaults to 1e-5

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

a LayerNorm1d class

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn.layer_norm import LayerNorm1d
test_conv = LayerNorm1d(4)
x = QTensor(np.arange(1,17).reshape([4,4]),requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355]
# ]

GroupNorm

class pyvqnet.nn.group_norm.GroupNorm(num_groups: int, num_channels: int, epsilon=1e-5, affine=True, dtype=None, name='')

Apply group normalization to a mini-batch of inputs. Input: \((N, C, *)\) where \(C=\text{num_channels}\) , Output: \((N, C, *)\) .

This layer implements the operation described in the paper Group Normalization

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

The input channels are divided into num_groups groups, each containing num_channels / num_groups channels. num_channels must be divisible by num_groups. The mean and standard deviation are computed separately for each group. If affine is True, then \(\gamma\) and \(\beta\) are learnable. Per-channel affine transformation parameter vector of size num_channels.

参数:

• (int) (num_channels) – Number of groups to split channels into

• (int) – Number of channels expected in the input

• eps – Value to add to the denominator for numerical stability. Default: 1e-5

• affine – A boolean value that, when set to True, causes this module to have learnable per-channel affine parameters, initialized to 1 (for weights) and 0 (for biases). Default: True.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

GroupNorm class

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet import kfloat32
from pyvqnet.nn import GroupNorm
test_conv = GroupNorm(2,10)
x = QTensor(np.arange(0,60*2*5).reshape([2,10,3,2,5]),requires_grad=True,dtype=kfloat32)
y = test_conv.forward(x)
print(y)

Linear

class pyvqnet.nn.Linear(input_channels, output_channels, weight_initializer=None, bias_initializer=None, use_bias=True, dtype=None, name: str = '')

Linear module (fully-connected layer). \(y = x@A.T + b\)

参数:

• input_channels – int - number of inputs features

• output_channels – int - number of output features

• weight_initializer – callable - defaults to normal

• bias_initializer – callable - defaults to zeros

• use_bias – bool - defaults to True

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

a Linear class

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Linear
c1 =2
c2 = 3
cin = 7
cout = 5
n = Linear(cin,cout)
input = QTensor(np.arange(1,c1*c2*cin+1).reshape((c1,c2,cin)),requires_grad=True,dtype=pyvqnet.kfloat32)
y = n.forward(input)
print(y)

# [
# [[4.3084583, -1.9228780, -0.3428757, 1.2840536, -0.5865945],
#  [9.8339605, -5.5135884, -3.1228657, 4.3025794, -4.1492314],
#  [15.3594627, -9.1042995, -5.9028554, 7.3211040, -7.7118683]],
# [[20.8849659, -12.6950111, -8.6828451, 10.3396301, -11.2745066],
#  [26.4104652, -16.2857227, -11.4628344, 13.3581581, -14.8371439],
#  [31.9359703, -19.8764324, -14.2428246, 16.3766804, -18.3997803]]
# ]

Dropout

class pyvqnet.nn.dropout.Dropout(dropout_rate=0.5)

Dropout module.The dropout module randomly sets the outputs of some units to zero, while upscale others according to the given dropout probability.

参数:

dropout_rate – float - probability that a neuron will be set to zero

返回:

a Dropout class

Example:

from pyvqnet.nn.dropout import Dropout
import numpy as np
from pyvqnet.tensor import QTensor
b = 2
ic = 2
x = QTensor(np.arange(-1*ic*2*2,(b-1)*ic*2*2).reshape([b,ic,2,2]),requires_grad=True)
droplayer = Dropout(0.5)
droplayer.train()
y = droplayer(x)
print(y)
# [[[[-16. -14.]
#    [-12.   0.]]

#   [[ -8.  -6.]
#    [ -4.  -2.]]]


#  [[[  0.   2.]
#    [  0.   6.]]

#   [[  0.   0.]
#    [  0.  14.]]]]

DropPath

class pyvqnet.nn.dropout.DropPath(dropout_rate=0.5, name='')

The DropPath module will drop paths (randomly deep) on a sample-by-sample basis.

参数:

• dropout_rate – float - The probability that the neuron is set to zero.

• name – The name of this module, the default is “”.

返回:

DropPath instance.

Example:

import pyvqnet.nn as nn
import pyvqnet.tensor as tensor

x = tensor.randu([4])
y = nn.DropPath()(x)
print(y)
#[0.9074978,0.9350062,0.6896403,0.3541051]

Pixel_Shuffle

class pyvqnet.nn.pixel_shuffle.Pixel_Shuffle(upscale_factors)

Rearrange tensors of shape: (, C * r^2, H, W) to a tensor of shape (, C, H * r, W * r) where r is the scaling factor.

参数:

upscale_factors – factor to increase the scale transformation

返回:

Pixel_Shuffle module

Example:

from pyvqnet.nn import Pixel_Shuffle
from pyvqnet.tensor import tensor
ps = Pixel_Shuffle(3)
inx = tensor.ones([5,2,3,18,4,4])
inx.requires_grad=  True
y = ps(inx)
print(y.shape)
#[5, 2, 3, 2, 12, 12]

Pixel_Unshuffle

class pyvqnet.nn.pixel_shuffle.Pixel_Unshuffle(downscale_factors)

Reverses the Pixel_Shuffle operation by rearranging the elements. Shuffles a Tensor of shape (, C, H * r, W * r) to (, C * r^2, H, W) , where r is the shrink factor.

参数:

downscale_factors – factor to increase the scale transformation

返回:

Pixel_Unshuffle module

Example:

from pyvqnet.nn import Pixel_Unshuffle
from pyvqnet.tensor import tensor
ps = Pixel_Unshuffle(3)
inx = tensor.ones([5, 2, 3, 2, 12, 12])
inx.requires_grad = True
y = ps(inx)
print(y.shape)
#[5, 2, 3, 18, 4, 4]

GRU

class pyvqnet.nn.gru.GRU(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Gated Recurrent Unit (GRU) module. Support multi-layer stacking, bidirectional configuration. The calculation formula of the single-layer one-way GRU is as follows:

\[\begin{split}\begin{array}{ll} r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)} \end{array}\end{split}\]

参数:

• input_size – Input feature dimensions.

• hidden_size – Hidden feature dimensions.

• num_layers – Stack layer numbers. default: 1.

• batch_first – If batch_first is True, input shape should be [batch_size,seq_len,feature_dim], if batch_first is False, the input shape should be [seq_len,batch_size,feature_dim],default: True.

• use_bias – If use_bias is False, this module will not contain bias. default: True.

• bidirectional – If bidirectional is True, the module will be bidirectional GRU. default: False.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

A GRU module instance.

Example:

from pyvqnet.nn import GRU
from pyvqnet.tensor import tensor

rnn2 = GRU(4, 6, 2, batch_first=False, bidirectional=True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])

output, hn = rnn2(input, h0)
print(output)
print(hn)
# [
# [[0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812]],
# [[0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840],
#  [0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840],
#  [0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840]],
# [[0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123],
#  [0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123],
#  [0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123]],
# [[0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759],
#  [0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759],
#  [0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759]],
# [[0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093]]
# ]
# [
# [[-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725],
#  [-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725],
#  [-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725]],
# [[-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730],
#  [-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730],
#  [-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730]],
# [[0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535]],
# [[-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812]]
# ]

RNN

class pyvqnet.nn.rnn.RNN(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Recurrent Neural Network (RNN) Module, use \(\tanh\) or \(\text{ReLU}\) as activation function. bidirectional RNN and multi-layer RNN is supported. The calculation formula of single-layer unidirectional RNN is as follows:

\[h_t = \tanh(W_{ih} x_t + b_{ih} + W_{hh} h_{(t-1)} + b_{hh})\]

If nonlinearity is 'relu', then \(\text{ReLU}\) will replace \(\tanh\).

参数:

• input_size – Input feature dimensions.

• hidden_size – Hidden feature dimensions.

• num_layers – Stack layer numbers. default: 1.

• nonlinearity – non-linear activation function, default: 'tanh' .

• batch_first – If batch_first is True, input shape should be [batch_size,seq_len,feature_dim], if batch_first is False, the input shape should be [seq_len,batch_size,feature_dim],default: True.

• use_bias – If use_bias is False, this module will not contain bias. default: True.

• bidirectional – If bidirectional is True, the module will be bidirectional RNN. default: False.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

A RNN module instance.

Example:

from pyvqnet.nn import RNN
from pyvqnet.tensor import tensor

rnn2 = RNN(4, 6, 2, batch_first=False, bidirectional = True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])
output, hn = rnn2(input, h0)
print(output)
print(hn)
# [
# [[-0.4481719, 0.4345263, 0.0284741, 0.6886298, 0.8672314, -0.3574123, 0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518],
#  [-0.4481719, 0.4345263, 0.0284741, 0.6886298, 0.8672314, -0.3574123, 0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518],
#  [-0.4481719, 0.4345263, 0.0284741, 0.6886298, 0.8672314, -0.3574123, 0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518]],
# [[-0.5737326, 0.1401956, -0.6656274, 0.3557707, 0.4083472, 0.3605195, 0.6767184, -0.2054843, -0.2875977, 0.6573941, -0.3289444, -0.1988498],
#  [-0.5737326, 0.1401956, -0.6656274, 0.3557707, 0.4083472, 0.3605195, 0.6767184, -0.2054843, -0.2875977, 0.6573941, -0.3289444, -0.1988498],
#  [-0.5737326, 0.1401956, -0.6656274, 0.3557707, 0.4083472, 0.3605195, 0.6767184, -0.2054843, -0.2875977, 0.6573941, -0.3289444, -0.1988498]],
# [[-0.4233001, 0.1252111, -0.7437832, 0.2092323, 0.5826398, 0.5207447, 0.7403980, -0.0006015, -0.4055642, 0.6553873, -0.0861093, -0.2096289],
#  [-0.4233001, 0.1252111, -0.7437832, 0.2092323, 0.5826398, 0.5207447, 0.7403980, -0.0006015, -0.4055642, 0.6553873, -0.0861093, -0.2096289],
#  [-0.4233001, 0.1252111, -0.7437832, 0.2092323, 0.5826398, 0.5207447, 0.7403980, -0.0006015, -0.4055642, 0.6553873, -0.0861093, -0.2096289]],
# [[-0.3636788, 0.3627384, -0.6542842, 0.0563165, 0.5711210, 0.5174620, 0.4968840, -0.3591014, -0.5738643, 0.7505787, -0.1767489, 0.2954176], [-0.3636788, 0.3627384, -0.6542842, 0.0563165, 0.5711210, 0.5174620, 0.4968840, -0.3591014, -0.5738643, 0.7505787, -0.1767489, 0.2954176], [-0.3636788, 0.3627384, -0.6542842, 0.0563165, 0.5711210, 0.5174620, 0.4968840, -0.3591014, -0.5738643, 0.7505787, -0.1767489, 0.2954176]],
# [[-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633, 0.4618312, -0.4173903, 0.1423969, -0.2332578, -0.4014739, 0.0601179],
#  [-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633, 0.4618312, -0.4173903, 0.1423969, -0.2332578, -0.4014739, 0.0601179],
#  [-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633, 0.4618312, -0.4173903, 0.1423969, -0.2332578, -0.4014739, 0.0601179]]
# ]
# [
# [[-0.1878589, -0.5177042, -0.3672480, 0.1613673, 0.4321197, 0.6168041],
#  [-0.1878589, -0.5177042, -0.3672480, 0.1613673, 0.4321197, 0.6168041],
#  [-0.1878589, -0.5177042, -0.3672480, 0.1613673, 0.4321197, 0.6168041]],
# [[-0.7923757, 0.0184400, -0.2851982, -0.6367047, 0.5933805, -0.6244841],
#  [-0.7923757, 0.0184400, -0.2851982, -0.6367047, 0.5933805, -0.6244841],
#  [-0.7923757, 0.0184400, -0.2851982, -0.6367047, 0.5933805, -0.6244841]],
# [[-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633],
#  [-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633],
#  [-0.1619987, 0.3079547, -0.5022690, -0.2989357, 0.2861646, 0.4965633]],
# [[0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518],
#  [0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518],
#  [0.8238092, -0.2751125, -0.4704098, 0.7624499, -0.4156595, -0.1646518]]
# ]

LSTM

class pyvqnet.nn.lstm.LSTM(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Long Short-Term Memory (LSTM) module. Support bidirectional LSTM, stacked multi-layer LSTM and other configurations. The calculation formula of single-layer unidirectional LSTM is as follows:

\[\begin{split}\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \\ h_t = o_t \odot \tanh(c_t) \\ \end{array}\end{split}\]

参数:

• input_size – Input feature dimensions.

• hidden_size – Hidden feature dimensions.

• num_layers – Stack layer numbers. default: 1.

• batch_first – If batch_first is True, input shape should be [batch_size,seq_len,feature_dim], if batch_first is False, the input shape should be [seq_len,batch_size,feature_dim],default: True.

• use_bias – If use_bias is False, this module will not contain bias. default: True.

• bidirectional – If bidirectional is True, the module will be bidirectional LSTM. default: False.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

A LSTM module instance.

Example:

from pyvqnet.nn import LSTM
from pyvqnet.tensor import tensor

rnn2 = LSTM(4, 6, 2, batch_first=False, bidirectional = True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])
c0 = tensor.ones([4, 3, 6])
output, (hn, cn) = rnn2(input, (h0, c0))

print(output)
print(hn)
print(cn)

# [
# [[0.1585344, 0.1758823, 0.4273642, 0.1640685, 0.1030634, 0.1657819, -0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487],
#  [0.1585344, 0.1758823, 0.4273642, 0.1640685, 0.1030634, 0.1657819, -0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487],
#  [0.1585344, 0.1758823, 0.4273642, 0.1640685, 0.1030634, 0.1657819, -0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487]],[[0.0366294, 0.1421610, 0.2401645, 0.0672358, 0.2205958, 0.1306419, 0.0129892, 0.1626964, 0.0116193, -0.1181969, -0.1101109, -0.0844855],
#  [0.0366294, 0.1421610, 0.2401645, 0.0672358, 0.2205958, 0.1306419, 0.0129892, 0.1626964, 0.0116193, -0.1181969, -0.1101109, -0.0844855],
#  [0.0366294, 0.1421610, 0.2401645, 0.0672358, 0.2205958, 0.1306419, 0.0129892, 0.1626964, 0.0116193, -0.1181969, -0.1101109, -0.0844855]],
# [[0.0169496, 0.1236289, 0.1416115, -0.0382225, 0.2277734, 0.0378894, 0.0252284, 0.1317508, 0.0191879, -0.0379719, -0.0707748, -0.0134158],
#  [0.0169496, 0.1236289, 0.1416115, -0.0382225, 0.2277734, 0.0378894, 0.0252284, 0.1317508, 0.0191879, -0.0379719, -0.0707748, -0.0134158],
#  [0.0169496, 0.1236289, 0.1416115, -0.0382225, 0.2277734, 0.0378894, 0.0252284, 0.1317508, 0.0191879, -0.0379719, -0.0707748, -0.0134158]],[[0.0223647, 0.1227054, 0.0959055, -0.1043864, 0.2314414, -0.0289589, 0.0346038, 0.1147739, 0.0461321, 0.0998507, 0.0097069, 0.0886721],
#  [0.0223647, 0.1227054, 0.0959055, -0.1043864, 0.2314414, -0.0289589, 0.0346038, 0.1147739, 0.0461321, 0.0998507, 0.0097069, 0.0886721],
#  [0.0223647, 0.1227054, 0.0959055, -0.1043864, 0.2314414, -0.0289589, 0.0346038, 0.1147739, 0.0461321, 0.0998507, 0.0097069, 0.0886721]],
# [[0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002, 0.0672482, 0.1278620, 0.1676001, 0.2955882, 0.2448514, 0.1802391],
#  [0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002, 0.0672482, 0.1278620, 0.1676001, 0.2955882, 0.2448514, 0.1802391],
#  [0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002, 0.0672482, 0.1278620, 0.1676001, 0.2955882, 0.2448514, 0.1802391]]
# ]
# [
# [[0.1687095, -0.2087553, 0.0254020, 0.3340017, 0.2515125, 0.2364762],
#  [0.1687095, -0.2087553, 0.0254020, 0.3340017, 0.2515125, 0.2364762],
#  [0.1687095, -0.2087553, 0.0254020, 0.3340017, 0.2515125, 0.2364762]],
# [[0.2621196, 0.2436198, -0.1790378, 0.0883382, -0.0479185, -0.0838870],
#  [0.2621196, 0.2436198, -0.1790378, 0.0883382, -0.0479185, -0.0838870],
#  [0.2621196, 0.2436198, -0.1790378, 0.0883382, -0.0479185, -0.0838870]],
# [[0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002],
#  [0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002],
#  [0.0345177, 0.1308527, 0.0884205, -0.1468191, 0.2236451, -0.0705002]],
# [[-0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487],
#  [-0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487],
#  [-0.0197110, 0.2073366, 0.0050953, -0.1467141, -0.1413236, -0.1404487]]
# ]
# [
# [[0.3588709, -0.3877619, 0.0519047, 0.5984558, 0.7709259, 1.0954115],
#  [0.3588709, -0.3877619, 0.0519047, 0.5984558, 0.7709259, 1.0954115],
#  [0.3588709, -0.3877619, 0.0519047, 0.5984558, 0.7709259, 1.0954115]],
# [[0.4557160, 0.6420789, -0.4407433, 0.1704233, -0.1592798, -0.1966903],
#  [0.4557160, 0.6420789, -0.4407433, 0.1704233, -0.1592798, -0.1966903],
#  [0.4557160, 0.6420789, -0.4407433, 0.1704233, -0.1592798, -0.1966903]],
# [[0.0681112, 0.4060420, 0.1333674, -0.3497016, 0.7122995, -0.1229735],
#  [0.0681112, 0.4060420, 0.1333674, -0.3497016, 0.7122995, -0.1229735],
#  [0.0681112, 0.4060420, 0.1333674, -0.3497016, 0.7122995, -0.1229735]],
# [[-0.0378819, 0.4589431, 0.0142352, -0.3194987, -0.3059436, -0.3285254],
#  [-0.0378819, 0.4589431, 0.0142352, -0.3194987, -0.3059436, -0.3285254],
#  [-0.0378819, 0.4589431, 0.0142352, -0.3194987, -0.3059436, -0.3285254]]
# ]

Dynamic_GRU

class pyvqnet.nn.gru.Dynamic_GRU(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Apply a multilayer gated recurrent unit (GRU) RNN to a dynamic-length input sequence.

The first input should be a variable-length batch sequence input defined Through the tensor.PackedSequence class. The tensor.PackedSequence class can be constructed as Call the next function in succession: pad_sequence, pack_pad_sequence.

The first output of Dynamic_GRU is also a tensor.PackedSequence class, It can be unpacked into a normal QTensor using tensor.pad_pack_sequence.

For each element in the input sequence, each layer computes the following formula:

\[\begin{split}\begin{array}{ll} r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)} \end{array}\end{split}\]

参数:

• input_size – Input feature dimension.

• hidden_size – Hidden feature dimension.

• num_layers – Number of loop layers. Default: 1

• batch_first – If True, the input shape is provided as [batch size, sequence length, feature dimension]. If False, input shape is provided as [sequence length, batch size, feature dimension], default True.

• use_bias – If False, the layer does not use bias weights b_ih and b_hh. Default: true.

• bidirectional – If true, becomes a bidirectional GRU. Default: false.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

A Dynamic_GRU class

Example:

from pyvqnet.nn import Dynamic_GRU
from pyvqnet.tensor import tensor
seq_len = [4,1,2]
input_size = 4
batch_size =3
hidden_size = 2
ml = 2
rnn2 = Dynamic_GRU(input_size,
                hidden_size=2,
                num_layers=2,
                batch_first=False,
                bidirectional=True)

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])

y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, hn = rnn2(input, h0)

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)
print(seq_unpacked)
print(lens_unpacked)
# [
# [[-0.3918380, 0.0056273, 0.9018179, 0.9006662],
#  [-0.3715909, 0.0307644, 0.9756137, 0.9705784],
#  [-0.3917399, 0.0057521, 0.9507942, 0.9456232]],
# [[-0.6348240, -0.0603764, 0.9014163, 0.8903066],
#  [0, 0, 0, 0],
#  [-0.6333261, -0.0592172, 0.9660671, 0.9580816]],
# [[-0.4571511, 0.0210018, 0.9151242, 0.9011748],
#  [0, 0, 0, 0],
#  [0, 0, 0, 0]],
# [[-0.3585358, 0.0918219, 0.9496037, 0.9391552],
#  [0, 0, 0, 0],
#  [0, 0, 0, 0]]
# ]
# [4 1 2]

Dynamic_RNN

class pyvqnet.nn.rnn.Dynamic_RNN(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Applies recurrent neural networks (RNNs) to dynamic-length input sequences.

The first input should be a variable-length batch sequence input defined Through the tensor.PackedSequence class. The tensor.PackedSequence class can be constructed as Call the next function in succession: pad_sequence, pack_pad_sequence.

The first output of Dynamic_RNN is also a tensor.PackedSequence class, It can be unpacked into a normal QTensor using tensor.pad_pack_sequence.

Recurrent Neural Network (RNN) module, using \(\tanh\) or \(\text{ReLU}\) as activation function. Support two-way, multi-layer configuration. The calculation formula of single-layer one-way RNN is as follows:

\[h_t = \tanh(W_{ih} x_t + b_{ih} + W_{hh} h_{(t-1)} + b_{hh})\]

If nonlinearity is 'relu', then \(\text{ReLU}\) will replace \(\tanh\).

参数:

• input_size – Input feature dimension.

• hidden_size – Hidden feature dimension.

• num_layers – Number of stacked RNN layers, default: 1.

• nonlinearity – Non-linear activation function, default is 'tanh'.

• batch_first – If True, the input shape is [batch size, sequence length, feature dimension], If False, the input shape is [sequence length, batch size, feature dimension], default True.

• use_bias – If False, the module does not apply bias items, default: True.

• bidirectional – If True, it becomes bidirectional RNN, default: False.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

Dynamic_RNN instance

Example:

from pyvqnet.nn import Dynamic_RNN
from pyvqnet.tensor import tensor
seq_len = [4,1,2]
input_size = 4
batch_size =3
hidden_size = 2
ml = 2
rnn2 = Dynamic_RNN(input_size,
                hidden_size=2,
                num_layers=2,
                batch_first=False,
                bidirectional=True,
                nonlinearity='relu')

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])

y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, hn = rnn2(input, h0)

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)
print(seq_unpacked)
print(lens_unpacked)

# [
# [[1.2980951, 0, 0, 0],
#  [1.5040692, 0, 0, 0],
#  [1.4927036, 0, 0, 0.1065927]],
# [[2.6561704, 0, 0, 0.2532321],
#  [0, 0, 0, 0],
#  [3.1472805, 0, 0, 0]],
# [[5.1231661, 0, 0, 0.7596353],
#  [0, 0, 0, 0],
#  [0, 0, 0, 0]],
# [[8.4954977, 0, 0, 0.8191229],
#  [0, 0, 0, 0],
#  [0, 0, 0, 0]]
# ]
# [4 1 2]

Dynamic_LSTM

class pyvqnet.nn.lstm.Dynamic_LSTM(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

Apply Long Short-Term Memory (LSTM) RNNs to dynamic-length input sequences.

The first input should be a variable-length batch sequence input defined Through the tensor.PackedSequence class. The tensor.PackedSequence class can be constructed as Call the next function in succession: pad_sequence, pack_pad_sequence.

The first output of Dynamic_LSTM is also a tensor.PackedSequence class, It can be unpacked into a normal QTensor using tensor.pad_pack_sequence.

Recurrent Neural Network (RNN) module, using \(\tanh\) or \(\text{ReLU}\) as activation function. Support two-way, multi-layer configuration. The calculation formula of single-layer one-way RNN is as follows:

\[\begin{split}\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \\ h_t = o_t \odot \tanh(c_t) \\ \end{array}\end{split}\]

参数:

• input_size – Input feature dimension.

• hidden_size – Hidden feature dimension.

• num_layers – Number of stacked LSTM layers, default: 1.

• batch_first – If True, the input shape is [batch size, sequence length, feature dimension], If False, the input shape is [sequence length, batch size, feature dimension], default True.

• use_bias – If False, the module does not apply bias items, default: True.

• bidirectional – If True, it becomes a bidirectional LSTM, default: False.

• dtype – The data type of the parameter, defaults: None, use the default data type kfloat32, which represents a 32-bit floating point number.

• name – name of the output layer

返回:

Dynamic_LSTM instance

Example:

from pyvqnet.nn import Dynamic_LSTM
from pyvqnet.tensor import tensor

input_size = 2
hidden_size = 2
ml = 2
seq_len = [3, 4, 1]
batch_size = 3
rnn2 = Dynamic_LSTM(input_size,
                    hidden_size=hidden_size,
                    num_layers=ml,
                    batch_first=False,
                    bidirectional=True)

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])
a.requires_grad = True
b.requires_grad = True
c.requires_grad = True
y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])
c0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, (hn, cn) = rnn2(input, (h0, c0))

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)

print(seq_unpacked)
print(lens_unpacked)

# [
# [[0.2038177, 0.1139005, 0.2312966, -0.1140076],
#  [0.1992285, 0.1221137, 0.2277344, -0.3147154],
#  [0.2293468, 0.0681745, 0.2426863, 0.2572871]],
# [[0.1398094, -0.0150359, 0.2513067, 0.0783743],
#  [0.1328388, -0.0031956, 0.2324090, -0.1962151],
#  [0, 0, 0, 0]],
# [[0.0898260, -0.0706460, 0.2396922, 0.2323916],
#  [0.0817787, -0.0449937, 0.2388873, -0.0000469],
#  [0, 0, 0, 0]],
# [[0, 0, 0, 0],
#  [0.0532839, -0.0870574, 0.2397324, 0.2103822],
#  [0, 0, 0, 0]]
# ]
# [3 4 1]

Interpolate

class pyvqnet.nn.Interpolate(size, scale_factor, mode='nearest', align_corners=None, recompute_scale_factor=None, name='')

Down/up samples the input.

Only four-dimensional input data is currently supported.

The input dimensions are interpreted in the form: B x C x H x W.

The modes available for resizing are: nearest 、bilinear 、bicubic.

参数:

• size – output spatial size.

• scale_factor – multiplier for spatial size.

• mode – algorithm used for upsampling nearest | bilinear | bicubic.

• align_corners – Geometrically, we consider the pixels of the input and output as squares rather than points. If set to True, the input and output tensors are aligned by the center points of their corner pixels, preserving the values at the corner pixels. If set to False, the input and output tensors are aligned by the corner points of their corner pixels, and the interpolation uses edge value padding for out-of-boundary values, making this operation independent of input size when scale_factor is kept the same. This only has an effect when mode is bilinear, bicubic.

• recompute_scale_factor – recompute the scale_factor for use in the interpolation calculation.

• name – Module name.

Example:

from pyvqnet.nn import Interpolate
from pyvqnet.tensor import tensor
import pyvqnet
pyvqnet.utils.set_random_seed(1)

import numpy as np
np.random.seed(0)

np_ = np.random.randn(36).reshape((1, 1, 6, 6)).astype(np.float32)
mode_ = "bilinear"
size_ = 3

class Model(pyvqnet.nn.Module):

    def __init__(self):
        super().__init__()
        self.inter = Interpolate(size = size_, mode=mode_)
        self.ln = pyvqnet.nn.Linear(9, 1)

    def forward(self, x):
        x = self.inter(x).reshape((1,-1))
        x = self.ln(x)
        return 2 * x

input_vqnet = tensor.QTensor(np_,  dtype=pyvqnet.kfloat32, requires_grad=True)
loss_pyvqnet = pyvqnet.nn.MeanSquaredError()
model_vqnet = Model()
output_vqnet = model_vqnet(input_vqnet)
l = loss_pyvqnet(tensor.QTensor([[1.0]]), output_vqnet)
l.backward()
print(model_vqnet.parameters()[0].grad)

fuse_module

class pyvqnet.nn.fuse_module(model)

It is used to fuse the corresponding neighbouring modules of the model in the reasoning stage into one module, which reduces the amount of computation in the model reasoning stage and increases the speed of model reasoning.

The currently supported module sequences are as follows:

conv, bn

linear, bn

The other sequences remain unchanged, for which the first module in the list is replaced with the fused module, and the others are replaced with Identity.

参数:

input – Includes modelling of fusion modules.

返回:

Module fused model.

Examples:

from pyvqnet import tensor
from pyvqnet.nn import Linear
from pyvqnet.nn import Module, BatchNorm1d, BatchNorm2d, Conv1D, Conv2D

from pyvqnet.qnn.vqc import *
from pyvqnet.optim import Adam
from pyvqnet.nn import Module,BinaryCrossEntropy, Sigmoid
from pyvqnet.data import data_generator
import numpy as np
from pyvqnet.tensor import QTensor

from time import time
from pyvqnet.utils import set_random_seed
from pyvqnet.nn import fuse_module

def get_accuary(result, label):
    result = (result > 0.5).astype(4)
    score = tensor.sums(result == label)
    return score.item()

class Model(Module):
    def __init__(self):

        super(Model, self).__init__()

        self.conv1 = Conv2D(1,2,1)
        self.ban = BatchNorm2d(2)

        self.conv2 = Conv2D(2,1,1)
        self.li1 = Linear(64,1)
        self.ac = Sigmoid()

    def forward(self, x):
        x = self.conv1(x)
        x = self.ban(x)
        x = self.conv2(x).reshape([-1,64])
        x = self.li1(x)
        x = self.ac(x)

        return x
X_train = np.random.randn(80, 1, 8, 8)
y_train = np.random.choice([0,1], size=(80))

model = Model().toGPU()
optimizer = Adam(model.parameters(), lr = 0.001)
batch_size = 20
epoch = 80
loss = BinaryCrossEntropy()
print("start training..............")
model.train()

loss_history = []
accuracy_history = []
time2 = time()

for i in range(epoch):
    count = 0
    sum_loss = 0
    accuary = 0
    t = 0
    for data, label in data_generator(X_train, y_train, batch_size, False):
        optimizer.zero_grad()
        data, label = QTensor(data,requires_grad=True).toGPU(), QTensor(label,
                                            dtype=6,
                                            requires_grad=False).toGPU()

        result = model(data)

        loss_b = loss(label.reshape([-1, 1]), result)

        loss_b.backward()
        optimizer._step()

        sum_loss += loss_b.item()
        count += batch_size
        accuary += get_accuary(result, label.reshape([-1,1]))
        t = t + 1

    loss_history.append(sum_loss/count)
    accuracy_history.append(accuary/count)
    print(
        f"epoch:{i}, #### loss:{sum_loss/count} #####accuray:{accuary/count}"
    )
print(f"run time {time() - time2}")


model.eval()

input = tensor.randn((20, 1, 8, 8)).toGPU()
print(list(model.named_children()))
time_a = time()
a = model(input)
print(f"fuse before {time() - time_a}")
fuse_module(model)
model.toGPU()
print(list(model.named_children()))
time_b = time()
b = model(input)
print(f"fuse after {time() - time_b}")

print(tensor.max(tensor.abs(a - b)).item())

SDPA

class pyvqnet.transformer.e2eqvit.SDPA(attn_mask=None, dropout_p=0., scale=None, is_causal=False)

SDPA scaling dot product attention mechanism, math method on cpu, flash method on gpu.

参数:

• attn_mask – Attention mask; shape must be broadcastable to the shape of attention weights.

• dropout_p – Dropout probability; if greater than 0.0, dropout is applied.

• scale – Scaling factor applied prior to softmax.

• is_causal – If true, assumes upper left causal attention masking and errors if both attn_mask and is_causal are set.

Examples:

from pyvqnet.transformer import SDPA
from pyvqnet import tensor
import pyvqnet
from time import time
import pyvqnet.nn as nn
import numpy as np

np.random.seed(42)

query_np = np.random.randn(3, 3, 3, 5).astype(np.float32)
key_np = np.random.randn(3, 3, 3, 5).astype(np.float32)
value_np = np.random.randn(3, 3, 3, 5).astype(np.float32)

model = SDPA(tensor.QTensor([1.])).toGPU()

query_p = tensor.QTensor(query_np, dtype=pyvqnet.kfloat32, requires_grad=True).toGPU()
key_p = tensor.QTensor(key_np, dtype=pyvqnet.kfloat32, requires_grad=True).toGPU()
value_p = tensor.QTensor(value_np, dtype=pyvqnet.kfloat32, requires_grad=True).toGPU()

out_sdpa = model(query_p, key_p, value_p)

out_sdpa.backward()

Loss Function Layer

备注

Please note that unlike pytorch and other frameworks, in the forward function of the following loss function, the first parameter is the label, and the second parameter is the predicted value.

MeanSquaredError

class pyvqnet.nn.MeanSquaredError

Creates a criterion that measures the mean squared error (squared L2 norm) between each element in the input \(x\) and target \(y\).

The unreduced loss can be described as:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = \left( x_n - y_n \right)^2,\]

where \(N\) is the batch size. , then:

\[\ell(x, y) = \operatorname{mean}(L)\]

\(x\) and \(y\) are QTensors of arbitrary shapes with a total of \(n\) elements each.

The mean operation still operates over all the elements, and divides by \(n\).

参数:

name – name of the output layer

返回:

a MeanSquaredError class

Parameters for loss forward function:

x: \((N, *)\) where \(*\) means, any number of additional dimensions

y: \((N, *)\), same shape as the input

Example:

from pyvqnet.tensor import QTensor
from pyvqnet import kfloat64
from pyvqnet.nn import MeanSquaredError
y = QTensor([[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]],
            requires_grad=False,
            dtype=kfloat64)
x = QTensor([[0.1, 0.05, 0.7, 0, 0.05, 0.1, 0, 0, 0, 0]],
            requires_grad=True,
            dtype=kfloat64)

loss_result = MeanSquaredError()
result = loss_result(y, x)
print(result)

# [0.0115000]

BinaryCrossEntropy

class pyvqnet.nn.BinaryCrossEntropy

Measures the Binary Cross Entropy between the target and the output:

The unreduced loss can be described as:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_n \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right],\]

where \(N\) is the batch size.

\[\ell(x, y) = \operatorname{mean}(L)\]

返回:

a BinaryCrossEntropy class

Parameters for loss forward function:

x: \((N, *)\) where \(*\) means, any number of additional dimensions

y: \((N, *)\), same shape as the input

Example:

import pyvqnet
from pyvqnet.tensor import QTensor
x = QTensor([[0.3, 0.7, 0.2], [0.2, 0.3, 0.1]], requires_grad=True)
y = QTensor([[0, 1.0, 0], [0, 0.0, 1]], requires_grad=True)

loss_result = pyvqnet.nn.BinaryCrossEntropy()
result = loss_result(y, x)
result.backward()
print(result)

# [0.6364825]

CategoricalCrossEntropy

class pyvqnet.nn.CategoricalCrossEntropy

This criterion combines LogSoftmax and NLLLoss in one single class.

The loss can be described as below, where class is index of target’s class:

\[\text{loss}(x, class) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

返回:

a CategoricalCrossEntropy class

Parameters for loss forward function:

x: \((N, *)\) where \(*\) means, any number of additional dimensions

y: \((N, *)\), same shape as the input, should have data type of the 64-bit integer.

Example:

from pyvqnet.tensor import QTensor
from pyvqnet import kfloat32,kint64
from pyvqnet.nn import CategoricalCrossEntropy
x = QTensor([[1, 2, 3, 4, 5],
[1, 2, 3, 4, 5],
[1, 2, 3, 4, 5]], requires_grad=True,dtype=kfloat32)
y = QTensor([[0, 1, 0, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 0, 0]], requires_grad=False,dtype=kint64)
loss_result = CategoricalCrossEntropy()
result = loss_result(y, x)
print(result)

# [3.7852428]

SoftmaxCrossEntropy

class pyvqnet.nn.SoftmaxCrossEntropy

This criterion combines LogSoftmax and NLLLoss in one single class with more numeral stablity.

The loss can be described as below, where class is index of target’s class:

\[\text{loss}(x, class) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

返回:

a SoftmaxCrossEntropy class

Parameters for loss forward function:

x: \((N, *)\) where \(*\) means, any number of additional dimensions

y: \((N, *)\), same shape as the input, should have data type of the 64-bit integer.

Example:

from pyvqnet.tensor import QTensor
from pyvqnet import kfloat32, kint64
from pyvqnet.nn import SoftmaxCrossEntropy
x = QTensor([[1, 2, 3, 4, 5], [1, 2, 3, 4, 5], [1, 2, 3, 4, 5]],
            requires_grad=True,
            dtype=kfloat32)
y = QTensor([[0, 1, 0, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 0, 0]],
            requires_grad=False,
            dtype=kint64)
loss_result = SoftmaxCrossEntropy()
result = loss_result(y, x)
result.backward()
print(result)

# [3.7852478]

NLL_Loss

class pyvqnet.nn.NLL_Loss

The average negative log likelihood loss. It is useful to train a classification problem with C classes

The x given through a forward call is expected to contain log-probabilities of each class. x has to be a Tensor of size either \((N, C)\) or \((N, C, d_1, d_2, ..., d_K)\) with \(K \geq 1\) for the K-dimensional case. The y that this loss expects should be a class index in the range \([0, C-1]\) where C = number of classes.

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - \sum_{n=1}^N \frac{1}{N}x_{n,y_n}, \quad\]

返回:

a NLL_Loss class

Parameters for loss forward function:

x: \((N, *)\), the output of the loss function, which can be a multidimensional variable.

y: \((N, *)\), the true value expected by the loss function, should have data type of the 64-bit integer.

Example:

from pyvqnet.tensor import QTensor
from pyvqnet import kfloat32,kint64
from pyvqnet.nn import NLL_Loss

x = QTensor([
    0.9476322568516703, 0.226547421131723, 0.5944201443911326,
    0.42830868492969476, 0.76414068655387, 0.00286059168094277,
    0.3574236812873617, 0.9096948856639084, 0.4560809854582528,
    0.9818027091583286, 0.8673569904602182, 0.9860275114020933,
    0.9232667066664217, 0.303693313961628, 0.8461034903175555
])
x= x.reshape([1, 3, 1, 5])
x.requires_grad = True
y = QTensor([[[2, 1, 0, 0, 2]]], dtype=kint64)

loss_result = NLL_Loss()
result = loss_result(y, x)
print(result)
#[-0.6187226]

CrossEntropyLoss

class pyvqnet.nn.CrossEntropyLoss

This criterion combines LogSoftmax and NLLLoss in one single class.

x is expected to contain raw, unnormalized scores for each class. x has to be a Tensor of size \((C)\) for unbatched input, \((N, C)\) or \((N, C, d_1, d_2, ..., d_K)\) with \(K \geq 1\) for the K-dimensional case.

The loss can be described as below, where class is index of target’s class:

\[\text{loss}(x, class) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

返回:

a CrossEntropyLoss class

Parameters for loss forward function:

x: \((N, *)\), the output of the loss function, which can be a multidimensional variable.

y: \((N, *)\), the true value expected by the loss function, should have data type of the 64-bit integer.

Example:

from pyvqnet.tensor import QTensor
from pyvqnet import kfloat32,kint64
from pyvqnet.nn import CrossEntropyLoss
x = QTensor([
    0.9476322568516703, 0.226547421131723, 0.5944201443911326,
    0.42830868492969476, 0.76414068655387, 0.00286059168094277,
    0.3574236812873617, 0.9096948856639084, 0.4560809854582528,
    0.9818027091583286, 0.8673569904602182, 0.9860275114020933,
    0.9232667066664217, 0.303693313961628, 0.8461034903175555
])
x.reshape_([1, 3, 1, 5])
x.requires_grad = True
y = QTensor([[[2, 1, 0, 0, 2]]], dtype=kint64)

loss_result = CrossEntropyLoss()
result = loss_result(y, x)
print(result)

#[1.1508200]

Activation Function

Activation

class pyvqnet.nn.activation.Activation

Base class of activation. Specific activation functions inherit this functions.

Sigmoid

class pyvqnet.nn.Sigmoid(name: str = '')

Applies a sigmoid activation function to the given layer.

\[\text{Sigmoid}(x) = \frac{1}{1 + \exp(-x)}\]

参数:

name – name of the output layer

返回:

sigmoid Activation layer

Examples:

from pyvqnet.nn import Sigmoid
from pyvqnet.tensor import QTensor
layer = Sigmoid()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.7310586, 0.8807970, 0.9525741, 0.9820138]

Softplus

class pyvqnet.nn.Softplus(name: str = '')

Applies the softplus activation function to the given layer.

\[\text{Softplus}(x) = \log(1 + \exp(x))\]

param name:

name of the output layer

return:

softplus Activation layer

Examples:

from pyvqnet.nn import Softplus
from pyvqnet.tensor import QTensor
layer = Softplus()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [1.3132616, 2.1269281, 3.0485873, 4.0181499]

Softsign

class pyvqnet.nn.Softsign(name: str = '')

Applies the softsign activation function to the given layer.

\[\text{SoftSign}(x) = \frac{x}{ 1 + |x|}\]

参数:

name – name of the output layer

返回:

softsign Activation layer

Examples:

from pyvqnet.nn import Softsign
from pyvqnet.tensor import QTensor
layer = Softsign()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.5000000, 0.6666667, 0.7500000, 0.8000000]

Softmax

class pyvqnet.nn.Softmax(axis: int = -1, name: str = '')

Applies a softmax activation function to the given layer.

\[\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

参数:

• axis – dimension on which to operate (-1 for last axis),default = -1

• name – name of the output layer

返回:

softmax Activation layer

Examples:

from pyvqnet.nn import Softmax
from pyvqnet.tensor import QTensor
layer = Softmax()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.0320586, 0.0871443, 0.2368828, 0.6439142]

HardSigmoid

class pyvqnet.nn.HardSigmoid(name: str = '')

Applies a hard sigmoid activation function to the given layer.

\[\begin{split}\text{Hardsigmoid}(x) = \begin{cases} 0 & \text{ if } x \le -3, \\ 1 & \text{ if } x \ge +3, \\ x / 6 + 1 / 2 & \text{otherwise} \end{cases}\end{split}\]

参数:

name – name of the output layer

返回:

hard sigmoid Activation layer

Examples:

from pyvqnet.nn import HardSigmoid
from pyvqnet.tensor import QTensor
layer = HardSigmoid()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.6666667, 0.8333334, 1, 1]

ReLu

class pyvqnet.nn.ReLu(name: str = '')

Applies a rectified linear unit activation function to the given layer.

\[\begin{split}\text{ReLu}(x) = \begin{cases} x, & \text{ if } x > 0\\ 0, & \text{ if } x \leq 0 \end{cases}\end{split}\]

参数:

name – name of the output layer

返回:

ReLu Activation layer

Examples:

from pyvqnet.nn import ReLu
from pyvqnet.tensor import QTensor
layer = ReLu()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [0, 2, 0, 4]

LeakyReLu

class pyvqnet.nn.LeakyReLu(alpha: float = 0.01, name: str = '')

Applies the leaky version of a rectified linear unit activation function to the given layer.

\[\begin{split}\text{LeakyRelu}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ \alpha * x, & \text{ otherwise } \end{cases}\end{split}\]

参数:

• alpha – LeakyRelu coefficient, default: 0.01

• name – name of the output layer

返回:

leaky ReLu Activation layer

Examples:

from pyvqnet.nn import LeakyReLu
from pyvqnet.tensor import QTensor
layer = LeakyReLu()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.0100000, 2, -0.0300000, 4]

Gelu

class pyvqnet.nn.Gelu(approximate='tanh', name='')

Apply Gaussian error linear unit function:

\[\text{GELU}(x) = x * \Phi(x)\]

When the approximation parameter is ‘tanh’, GELU is estimated by:

\[\text{GELU}(x) = 0.5 * x * (1 + \text{Tanh}(\sqrt{2 / \pi} * (x + 0.044715 * x^3)))\]

参数:

• approximate – Approximate calculation method, default is “tanh”.

• name – Name of the activation function layer, default is “”.

返回:

Gelu activation function layer instance.

Examples:

from pyvqnet.tensor import randu, ones_like
from pyvqnet.nn import Gelu
qa = randu([5,4])
qb = Gelu()(qa)
print(qb)
# [[0.0292515,0.0668998,0.4036024,0.8369502],
# [0.1929213,0.1981275,0.2358531,0.7790835],
# [0.1754935,0.6204091,0.2354677,0.2409406],
# [0.4238827,0.804715,0.1633414,0.2853],
# [0.1959854,0.590143,0.553995,0.0008423]]

ELU

class pyvqnet.nn.ELU(alpha: float = 1.0, name: str = '')

Applies the exponential linear unit activation function to the given layer.

\[\begin{split}\text{ELU}(x) = \begin{cases} x, & \text{ if } x > 0\\ \alpha * (\exp(x) - 1), & \text{ if } x \leq 0 \end{cases}\end{split}\]

参数:

• alpha – Elu coefficient, default: 1.0

• name – name of the output layer

返回:

Elu Activation layer

Examples:

from pyvqnet.nn import ELU
from pyvqnet.tensor import QTensor
layer = ELU()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.6321205, 2, -0.9502130, 4]

Tanh

class pyvqnet.nn.Tanh(name: str = '')

Applies the hyperbolic tangent activation function to the given layer.

\[\text{Tanh}(x) = \frac{\exp(x) - \exp(-x)} {\exp(x) + \exp(-x)}\]

参数:

name – name of the output layer

返回:

hyperbolic tangent Activation layer

Examples:

from pyvqnet.nn import Tanh
from pyvqnet.tensor import QTensor
layer = Tanh()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.7615942, 0.9640276, -0.9950548, 0.9993293]

Optimizer Module

Optimizer

class pyvqnet.optim.optimizer.Optimizer(params, lr=0.01)

Base class for all optimizers.

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

adadelta

class pyvqnet.optim.adadelta.Adadelta(params, lr=0.01, beta=0.99, epsilon=1e-8)

ADADELTA: An Adaptive Learning Rate Method. reference: (https://arxiv.org/abs/1212.5701)

\[\begin{split}E(g_t^2) &= \beta * E(g_{t-1}^2) + (1-\beta) * g^2\\ Square\_avg &= \sqrt{ ( E(dx_{t-1}^2) + \epsilon ) / ( E(g_t^2) + \epsilon ) }\\ E(dx_t^2) &= \beta * E(dx_{t-1}^2) + (1-\beta) * (-g*square\_avg)^2 \\ param\_new &= param - lr * Square\_avg\end{split}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• beta – for computing a running average of squared gradients (default: 0.99)

• epsilon – term added to the denominator to improve numerical stability (default: 1e-8)

返回:

a Adadelta optimizer

Example:

import numpy as np
from pyvqnet.optim import adadelta
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1, 2, 3, 4).astype(np.float64))
params = [param]
opti = adadelta.Adadelta(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9999900, 1.9999900, 2.9999900],
#  [3.9999900, 4.9999900, 5.9999900, 6.9999900],
#  [7.9999900, 8.9999905, 9.9999905, 10.9999905]],
# [[11.9999905, 12.9999905, 13.9999905, 14.9999905],
#  [15.9999905, 16.9999905, 17.9999905, 18.9999905],
#  [19.9999905, 20.9999905, 21.9999905, 22.9999905]]]
# ]

# [
# [[[0, 0.9999800, 1.9999800, 2.9999800],
#  [3.9999800, 4.9999800, 5.9999800, 6.9999800],
#  [7.9999800, 8.9999800, 9.9999800, 10.9999800]],
# [[11.9999800, 12.9999800, 13.9999800, 14.9999800],
#  [15.9999800, 16.9999809, 17.9999809, 18.9999809],
#  [19.9999809, 20.9999809, 21.9999809, 22.9999809]]]
# ]

adagrad

class pyvqnet.optim.adagrad.Adagrad(params, lr=0.01, epsilon=1e-8)

Implements Adagrad algorithm. reference: (https://databricks.com/glossary/adagrad)

\[\begin{split}\begin{align} moment\_new &= moment + g * g\\param\_new &= param - \frac{lr * g}{\sqrt{moment\_new} + \epsilon} \end{align}\end{split}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• epsilon – term added to the denominator to improve numerical stability (default: 1e-8)

返回:

a Adagrad optimizer

Example:

import numpy as np
from pyvqnet.optim import adagrad
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1, 2, 3, 4).astype(np.float64))
params = [param]
opti = adagrad.Adagrad(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0, 0.9829289, 1.9829290, 2.9829290],
#  [3.9829290, 4.9829288, 5.9829288, 6.9829288],
#  [7.9829288, 8.9829283, 9.9829283, 10.9829283]],
# [[11.9829283, 12.9829283, 13.9829283, 14.9829283],
#  [15.9829283, 16.9829292, 17.9829292, 18.9829292],
#  [19.9829292, 20.9829292, 21.9829292, 22.9829292]]]
# ]

AdamW

class pyvqnet.optim.adam.AdamW(params, lr=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8, weight_decay=0.01, amsgrad: bool = False)

Implement the AdamW algorithm.

\[t=t+1\]

\[param\_new = param - lr*weight\_decay*param\]

\[moment\_1\_new=\beta1*moment\_1+(1−\beta1)g\]

\[moment\_2\_new=\beta2*moment\_2+(1−\beta2)g*g\]

\[lr = lr*\frac{\sqrt{1-\beta2^t}}{1-\beta1^t}\]

If the parameter amsgrad is True

\[moment\_2\_max = max(moment\_2\_max,moment\_2)\]

\[param\_new=param\_new-lr*\frac{moment\_1}{\sqrt{moment\_2\_max}+\epsilon}\]

otherwise:

\[param\_new=param\_new-lr*\frac{moment\_1}{\sqrt{moment\_2}+\epsilon}\]

参数:

• params – Model parameters that need to be optimized.

• lr – learning rate (default: 0.01).

• beta1 – Coefficient used to calculate the running average of the gradient and its square (default: 0.9).

• beta2 – Coefficient used to calculate the running average of the gradient and its square (default: 0.999).

• epsilon – Constant to add to the denominator to improve numerical stability (default: 1e-8).

• weight_decay – Weight decay coefficient, default 0.01.

• amsgrad – Whether to use the AMSGrad variant of this algorithm (default: False).

返回:

An AdamW optimizer.

Example:

from pyvqnet.optim import adam
import numpy as np
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = adam.AdamW(params, lr=0.5)

for i in range(1,3):
    opti.step()
print(param)
# [[[[ 0. ,-0.007475 , 0.98255 , 1.972575 ],
# [2.9626, 3.952625, 4.9426501, 5.9326751],
# [6.9227001, 7.9127251, 8.9027501, 9.8927751]],

# [[10.8828001,11.8728251,12.8628501,13.8528751],
# [14.8429002,15.8329252,16.8229502,17.8129752],
# [18.8030002,19.7930252,20.7830502,21.7730752]]]]

Adam

class pyvqnet.optim.adam.Adam(params, lr=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8, weight_decay=0, amsgrad: bool = False)

Adam: A Method for Stochastic Optimization reference: (https://arxiv.org/abs/1412.6980),it can dynamically adjusts the learning rate of each parameter using the 1st moment estimates and the 2nd moment estimates of the gradient.

\[t = t + 1\]

\[param = param - lr*weight\_decay*param\]

\[moment\_1\_new=\beta1∗moment\_1+(1−\beta1)g\]

\[moment\_2\_new=\beta2∗moment\_2+(1−\beta2)g*g\]

\[lr = lr*\frac{\sqrt{1-\beta2^t}}{1-\beta1^t}\]

if amsgrad = True

\[moment\_2\_max = max(moment\_2\_max,moment\_2)\]

\[param\_new=param-lr*\frac{moment\_1}{\sqrt{moment\_2\_max}+\epsilon}\]

else

\[param\_new=param-lr*\frac{moment\_1}{\sqrt{moment\_2}+\epsilon}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• beta1 – coefficients used for computing running averages of gradient and its square (default: 0.9)

• beta2 – coefficients used for computing running averages of gradient and its square (default: 0.999)

• epsilon – term added to the denominator to improve numerical stability (default: 1e-8)

• weight_decay – Weight decay coefficient, default 0.

• amsgrad – whether to use the AMSGrad variant of this algorithm (default: False)

返回:

a Adam optimizer

Example:

import numpy as np
from pyvqnet.optim import adam
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1, 2, 3, 4).astype(np.float64))
params = [param]
opti = adam.Adam(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0, 0.9800000, 1.9800000, 2.9800000],
#  [3.9800000, 4.9799995, 5.9799995, 6.9799995],
#  [7.9799995, 8.9799995, 9.9799995, 10.9799995]],
# [[11.9799995, 12.9799995, 13.9799995, 14.9799995],
#  [15.9799995, 16.9799995, 17.9799995, 18.9799995],
#  [19.9799995, 20.9799995, 21.9799995, 22.9799995]]]
# ]

adamax

class pyvqnet.optim.adamax.Adamax(params, lr=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8)

Implements Adamax algorithm (a variant of Adam based on infinity norm).reference: (https://arxiv.org/abs/1412.6980)

\[\begin{split}\\t = t + 1\end{split}\]

\[moment\_new=\beta1∗moment+(1−\beta1)g\]

\[norm\_new = \max{(\beta1∗norm+\epsilon, \left|g\right|)}\]

\[lr = \frac{lr}{1-\beta1^t}\]

\[\begin{split}param\_new = param − lr*\frac{moment\_new}{norm\_new}\\\end{split}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• beta1 – coefficients used for computing running averages of gradient and its square (default: 0.9)

• beta2 – coefficients used for computing running averages of gradient and its square (default: 0.999)

• epsilon – term added to the denominator to improve numerical stability (default: 1e-8)

返回:

a Adamax optimizer

Example:

import numpy as np
from pyvqnet.optim import adamax
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = adamax.Adamax(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0, 0.9800000, 1.9800000, 2.9800000],
#  [3.9800000, 4.9799995, 5.9799995, 6.9799995],
#  [7.9799995, 8.9799995, 9.9799995, 10.9799995]],
# [[11.9799995, 12.9799995, 13.9799995, 14.9799995],
#  [15.9799995, 16.9799995, 17.9799995, 18.9799995],
#  [19.9799995, 20.9799995, 21.9799995, 22.9799995]]]
# ]

rmsprop

class pyvqnet.optim.rmsprop.RMSProp(params, lr=0.01, beta=0.99, epsilon=1e-8)

Implements RMSprop algorithm. reference: (https://arxiv.org/pdf/1308.0850v5.pdf)

\[s_{t+1} = s_{t} + (1 - \beta)*(g)^2\]

\[param_new = param - \frac{g}{\sqrt{s_{t+1}} + epsilon}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• beta – coefficients used for computing running averages of gradient and its square (default: 0.99)

• epsilon – term added to the denominator to improve numerical stability (default: 1e-8)

返回:

a RMSProp optimizer

Example:

import numpy as np
from pyvqnet.optim import rmsprop
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = rmsprop.RMSProp(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9000000, 1.9000000, 2.8999999],
#  [3.8999999, 4.9000001, 5.9000001, 6.9000001],
#  [7.9000001, 8.8999996, 9.8999996, 10.8999996]],
# [[11.8999996, 12.8999996, 13.8999996, 14.8999996],
#  [15.8999996, 16.8999996, 17.8999996, 18.8999996],
#  [19.8999996, 20.8999996, 21.8999996, 22.8999996]]]
# ]

# [
# [[[0, 0.8291118, 1.8291118, 2.8291118],
#  [3.8291118, 4.8291121, 5.8291121, 6.8291121],
#  [7.8291121, 8.8291111, 9.8291111, 10.8291111]],
# [[11.8291111, 12.8291111, 13.8291111, 14.8291111],
#  [15.8291111, 16.8291111, 17.8291111, 18.8291111],
#  [19.8291111, 20.8291111, 21.8291111, 22.8291111]]]
# ]

sgd

class pyvqnet.optim.sgd.SGD(params, lr=0.01, momentum=0, nesterov=False)

Implements SGD algorithm. reference: (https://en.wikipedia.org/wiki/Stochastic_gradient_descent)

\[\begin{split}\\param\_new=param-lr*g\\\end{split}\]

参数:

• params – params of model which need to be optimized

• lr – learning_rate of model (default: 0.01)

• momentum – momentum factor (default: 0)

• nesterov – enables Nesterov momentum (default: False)

返回:

a SGD optimizer

Example:

import numpy as np
from pyvqnet.optim import sgd
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = sgd.SGD(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0, 0.9900000, 1.9800000, 2.9700000],
#  [3.9600000, 4.9499998, 5.9400001, 6.9299998],
#  [7.9200001, 8.9099998, 9.8999996, 10.8900003]],
# [[11.8800001, 12.8699999, 13.8599997, 14.8500004],
#  [15.8400002, 16.8299999, 17.8199997, 18.8099995],
#  [19.7999992, 20.7900009, 21.7800007, 22.7700005]]]
# ]

# [
# [[[0, 0.9800000, 1.9600000, 2.9400001],
#  [3.9200001, 4.8999996, 5.8800001, 6.8599997],
#  [7.8400002, 8.8199997, 9.7999992, 10.7800007]],
# [[11.7600002, 12.7399998, 13.7199993, 14.7000008],
#  [15.6800003, 16.6599998, 17.6399994, 18.6199989],
#  [19.5999985, 20.5800018, 21.5600014, 22.5400009]]]
# ]

rotosolve

Rotosolve algorithm, which allows a direct jump to the optimal value of a single parameter relative to the fixed value of other parameters, can directly find the optimal parameters of the quantum circuit optimization algorithm.

class pyvqnet.optim.rotosolve.Rotosolve(max_iter=50)

Rotosolve: The rotosolve algorithm can be used to minimize a linear combination of quantum measurement expectation values. See the following paper: https://arxiv.org/abs/1903.12166, Ken M. Nakanishi. https://arxiv.org/abs/1905.09692, Mateusz Ostaszewski.

参数:

max_iter – max number of iterations of the rotosolve update

返回:

a Rotosolve optimizer

Example:

from pyvqnet.optim.rotosolve import Rotosolve
import pyqpanda as pq
from pyvqnet.tensor import QTensor

from pyvqnet import kfloat64
from pyvqnet.qnn.measure import expval
machine = pq.CPUQVM()
machine.init_qvm()
nqbits = machine.qAlloc_many(2)


def gen(param, generators, qbits, circuit):
    if generators == "X":
        circuit.insert(pq.RX(qbits, param))
    elif generators == "Y":
        circuit.insert(pq.RY(qbits, param))
    else:
        circuit.insert(pq.RZ(qbits, param))


def circuits(params, generators, circuit):
    gen(params[0], generators[0], nqbits[0], circuit)
    gen(params[1], generators[1], nqbits[1], circuit)
    circuit.insert(pq.CNOT(nqbits[0], nqbits[1]))
    prog = pq.QProg()
    prog.insert(circuit)
    return prog


def ansatz1(params: QTensor, generators):
    circuit = pq.QCircuit()
    params = params.getdata()
    prog = circuits(params, generators, circuit)
    return expval(machine, prog, {"Z0": 1},
                nqbits), expval(machine, prog, {"Y1": 1}, nqbits)


def ansatz2(params: QTensor, generators):
    circuit = pq.QCircuit()
    params = params.getdata()
    prog = circuits(params, generators, circuit)
    return expval(machine, prog, {"X0": 1}, nqbits)


def loss(params):
    Z, Y = ansatz1(params, ["X", "Y"])
    X = ansatz2(params, ["X", "Y"])
    return 0.5 * Y + 0.8 * Z - 0.2 * X


t = QTensor([0.3, 0.25],dtype=kfloat64)
opt = Rotosolve(max_iter=5)

costs_rotosolve = opt.minimize(t, loss)
print(costs_rotosolve)
# [0.7642691884821847, -0.799999999999997, -0.799999999999997, -0.799999999999997, -0.799999999999997]

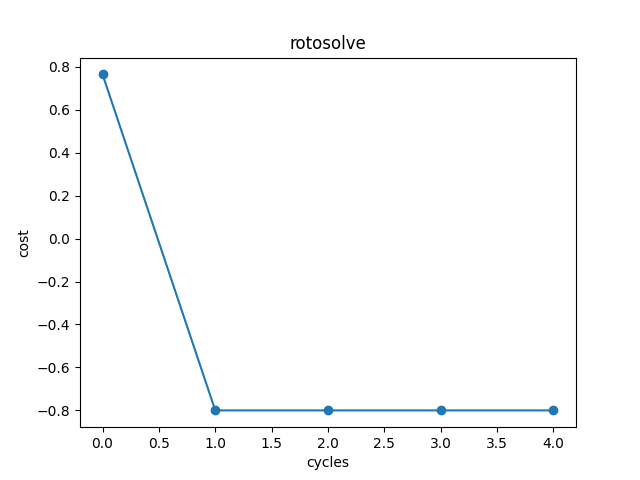
Metrics

MSE

class pyvqnet.utils.metrics.MSE(y_true_Qtensor, y_pred_Qtensor)

MSE: Mean Squared Error.

参数:

• y_true_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), true target value.

• y_pred_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), estimated target values.

返回:

return with float result.

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.MSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 9.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.MSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 9.0

RMSE

class pyvqnet.utils.metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)

RMSE: Root Mean Squared Error.

参数:

• y_true_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), true target value.

• y_pred_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), estimated target values.

返回:

return with float result.

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

MAE

class pyvqnet.utils.metrics.MAE(y_true_Qtensor, y_pred_Qtensor)

MAE: Mean Absolute Error.

参数:

• y_true_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), true target value.

• y_pred_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), estimated target values.

返回:

return with float result.

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.MAE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.MAE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

R_Square

class pyvqnet.utils.metrics.R_Square(y_true_Qtensor, y_pred_Qtensor, sample_weight=None)

R_Square: R^2 (coefficient of determination) regression score function. The best possible score is 1.0, which can be negative (since the model can deteriorate arbitrarily). One that always predicts the expected value of y, ignoring the input features, will get an R^2 score of 0.0.

参数:

• y_true_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), true target value.

• y_pred_Qtensor – A QTensor of shape like (n_samples,) or (n_samples, n_outputs), estimated target values.

• sample_weight – Array of shape like (n_samples,), optional sample weight, default:None.

返回:

return with float result.

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.R_Square(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 0.09999999999999998

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.R_Square(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 0.15625

precision_recall_f1_2_score

class pyvqnet.utils.metrics.precision_recall_f1_2_score(y_true_Qtensor, y_pred_Qtensor)

Calculate the precision, recall and F1 score of the predicted values under the 2-classification task. The predicted and true values need to be QTensors of similar shape (n_samples, ), with a value of 0 or 1, representing the labels of the two classes.

参数:

• y_true_Qtensor – A 1D QTensor, true target value.

• y_pred_Qtensor – A 1D QTensor, estimated target value.

返回:

• precision - precision result

• recall - recall result

• f1 - f1 score

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.QTensor([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
y_pred_Qtensor = tensor.QTensor([0, 0, 1, 1, 1, 0, 0, 1, 1, 1])

precision, recall, f1 = vqnet_metrics.precision_recall_f1_2_score(
    y_true_Qtensor, y_pred_Qtensor)
print(precision, recall, f1)
# 0.5 0.6 0.5454545454545454

precision_recall_f1_N_score

class pyvqnet.utils.metrics.precision_recall_f1_N_score(y_true_Qtensor, y_pred_Qtensor, N, average)

Precision, recall, and F1 score calculations for multi-classification tasks. where the predicted value and the true value are QTensors of similar shape (n_samples, ), and the values are integers from 0 to N-1, representing the labels of N classes.

参数:

• y_true_Qtensor – A 1D QTensor, true target value.

• y_pred_Qtensor – A 1D QTensor, estimated target value.

• N – N classes (number of classes).

• average –

  string, [‘micro’, ‘macro’, ‘weighted’]. This parameter is required for multi-class/multi-label targets.

  'micro': Compute metrics globally by counting total true counts, false negatives and false positives.

  'macro': Calculate the metric for each label and find its unweighted value. Meaning that the balance of labels is not considered.

  'weighted': Calculate the metrics for each label and find their average (the number of true instances of each label). This changes 'macro' to account for label imbalance; this may result in F-scores not being between precision and recall.

返回:

• precision - precision result

• recall - recall result

• f1 - f1 score

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

reference_list = [1, 1, 2, 2, 2, 3, 3, 3, 3, 3]
prediciton_list = [1, 2, 2, 2, 3, 1, 2, 3, 3, 3]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

precision_micro, recall_micro, f1_micro = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='micro')
print(precision_micro, recall_micro, f1_micro)
# 0.6 0.6 0.6

precision_macro, recall_macro, f1_macro = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='macro')
print(precision_macro, recall_macro, f1_macro)
# 0.5833333333333334 0.5888888888888889 0.5793650793650794

precision_weighted, recall_weighted, f1_weighted = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='weighted')
print(precision_weighted, recall_weighted, f1_weighted)
# 0.625 0.6 0.6047619047619047

precision_recall_f1_Multi_score

class pyvqnet.utils.metrics.precision_recall_f1_Multi_score(y_true_Qtensor, y_pred_Qtensor, N, average)

Precision, recall, and F1 score calculations for multi-classification tasks. where the predicted and true values are QTensors of similar shape (n_samples, N), where the values are N-dimensional one-hot encoded label values.

参数:

• y_true_Qtensor – A 1D QTensor, true target value.

• y_pred_Qtensor – A 1D QTensor, estimated target value.

• N – N classes (number of classes).

• average –

  string, [‘micro’, ‘macro’, ‘weighted’]. This parameter is required for multi-class/multi-label targets.

  'micro': Compute metrics globally by counting total true counts, false negatives and false positives.

  'macro': Calculate the metric for each label and find its unweighted value. Meaning that the balance of labels is not considered.

  'weighted': Calculate the metrics for each label and find their average (the number of true instances of each label). This changes 'macro' to account for label imbalance; this may result in F-scores not being between precision and recall.

返回:

• precision - precision result

• recall - recall result

• f1 - f1 score

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

reference_list = [[1, 0], [0, 1], [0, 0], [1, 1], [1, 0]]
prediciton_list = [[1, 0], [0, 0], [1, 0], [0, 0], [0, 0]]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

micro_precision, micro_recall, micro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='micro')
print(micro_precision, micro_recall, micro_f1)
# 0.5 0.2 0.28571428571428575

macro_precision, macro_recall, macro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='macro')
print(macro_precision, macro_recall, macro_f1)
# 0.25 0.16666666666666666 0.2

weighted_precision, weighted_recall, weighted_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='weighted')
print(weighted_precision, weighted_recall, weighted_f1)
# 0.3 0.19999999999999998 0.24

reference_list = [[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 0], [1, 0, 1]]
prediciton_list = [[1, 0, 0], [1, 0, 0], [1, 1, 1], [1, 0, 0], [0, 1, 1]]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

micro_precision, micro_recall, micro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='micro')
print(micro_precision, micro_recall, micro_f1) # 0.5 0.5714285714285714 0.5333333333333333

macro_precision, macro_recall, macro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='macro')
print(macro_precision, macro_recall, macro_f1)
# 0.5 0.5555555555555555 0.5238095238095238

weighted_precision, weighted_recall, weighted_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='weighted')
print(weighted_precision, weighted_recall, weighted_f1)
# 0.5 0.5714285714285714 0.5306122448979592

auc_calculate

class pyvqnet.utils.metrics.auc_calculate(y_true_Qtensor, y_pred_Qtensor, pos_label=None, sample_weight=None, drop_intermediate=True)

Compute the precision, recall and f1 score of the classification task.

参数:

• y_true_Qtensor – A QTensor like of shape [n_samples]. A true binary label. If the label is not {1,1} or {0,1}, pos_label should be given explicitly.

• y_pred_Qtensor – A QTensor like of shape [n_samples]. Target score, which can be a positive probability estimate class, confidence value, or a non-threshold measure of the decision (returned by “decision_function” on some classifiers)

• pos_label – int or str. The label of the positive class. default=None. When pos_label is None, if y_true_Qtensor is at {-1,1} or {0,1}, pos_label is set to 1, otherwise an error will be raised.

• sample_weight – array of shape (n_samples,), default=None.

• drop_intermediate – boolean, optional (default=True). Whether to lower some suboptimal thresholds that don’t appear on the drawn ROC curve.

返回:

output float result.

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y = np.array([1, 1, 1, 1, 0, 1, 0, 0, 0, 0])
pred = np.array([0.9, 0.8, 0.7, 0.6, 0.6, 0.4, 0.4, 0.3, 0.2, 0.1])
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor)
print("auc:", result)
# 0.92

y = np.array([1, 1, 1, 1, 1, 0, 0, 1, 1, 1])
pred = np.array([1, 0, 1, 1, 1, 1, 0, 1, 1, 0])
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor)
print("auc:", result)
# 0.625

y = [1, 2, 1, 1, 1, 0, 0, 1, 1, 1]
pred = [1, 0, 2, 1, 1, 1, 0, 1, 1, 0]
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor, pos_label=2)
print("auc:", result)
# 0.1111111111111111

VQNet Naive Distributed Computing Module

Environment deployment

The following describes the VQNet deployment of the environment under the Linux system based on CPU and GPU distributed computing, respectively.

MPI Installation

MPI is a common library for inter-CPU communication, and the distributed computing function of CPU in VQNet is realized based on MPI, and the following section describes how to install MPI in Linux system (at present, the distributed computing function based on CPU is realized only on Linux).

Detect if gcc, gfortran compilers are installed.

which gcc
which gfortran

When the paths to gcc and gfortran are shown, you can proceed to the next step of installation, if you do not have the corresponding compilers, please install the compilers first. When the compilers have been checked, use the wget command to download them.

wget http://www.mpich.org/static/downloads/3.3.2/mpich-3.3.2.tar.gz
tar -zxvf mpich-3.3.2.tar.gz
cd mpich-3.3.2
./configure --prefix=/usr/local/mpich
make
make install

Finish compiling and installing mpich and configure its environment variables.

vim ~/.bashrc

# At the bottom of the document, add
export PATH="/usr/local/mpich/bin:$PATH"

After saving and exiting, use source to execute

source ~/.bashrc

Use which to verify that the environment variables are configured correctly. If the path is displayed, the installation has completed successfully.

In addition, you can install mpi4py via pip install, if you get the following error

To solve the problem of incompatibility between mpi4py and python versions, you can do the following

# Staging the compiler for the current python environment with the following code
pushd /root/anaconda3/envs/$CONDA_DEFAULT_ENV/compiler_compat && mv ld ld.bak && popd

# Re-installation
pip install mpi4py

# reduction
pushd /root/anaconda3/envs/$CONDA_DEFAULT_ENV/compiler_compat && mv ld.bak ld && popd

NCCL Installation

NCCL is a common library for communication between GPUs, and the distributed computing function of GPUs in VQNet is realized based on NCCL, and the following introduces how to install NCCL in Linux system (at present, the distributed computing function based on GPUs is realized only on Linux). This section requires MPI support, so the MPI environment needs to be deployed as well.

Pull the NCCL repositories from github to local

git clone https://github.com/NVIDIA/nccl.git

Go to the nccl root directory and compile

cd nccl
make -j src.build

If cuda is not installed in the default path /usr/local/cuda, you need to define the path to CUDA, and compile it using the following code

make src.build CUDA_HOME=<path to cuda install>

And you can specify the installation directory according to BUILDDIR, the command is as follows

make src.build CUDA_HOME=<path to cuda install> BUILDDIR=/usr/local/nccl

Add configuration to the .bashrc file after installation is complete

vim ~/.bashrc

# Add at the bottom
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/nccl/lib
export PATH=$PATH:/usr/local/nccl/bin

After saving, execute

source ~/.bashrc

It can be verified with nccl-test

git clone https://github.com/NVIDIA/nccl-tests.git
cd nccl-tests
make -j12 CUDA_HOME=/usr/local/cuda
./build/all_reduce_perf -b 8 -e 256M -f 2 -g 1

Inter-node communication environment deployment

To implement distributed computing on multiple nodes, first you need to ensure the consistency of the mpich environment and the python environment on multiple nodes, and secondly, you need to set up secret-free communication between nodes. .. code-block:

# Execute on each node
ssh-keygen

# After that, keep entering to generate a public key (id_rsa.pub) and a private key (id_rsa) in the .ssh folder
# Add the public keys of both of its other nodes to the authorized_keys file of the first node.
# Then pass the authorized_keys file from the first node to the other two nodes to achieve password-free communication between the nodes.
# Execute on child node node1
cat ~/.ssh/id_dsa.pub >> node0:~/.ssh/authorized_keys

# Execute on child node node2
cat ~/.ssh/id_dsa.pub >> node0:~/.ssh/authorized_keys

# After deleting the authorized_keys files on node1 and node2, copy the authorized_keys file on node0 to the other two nodes.
scp ~/.ssh/authorized_keys  node1:~/.ssh/authorized_keys
scp ~/.ssh/authorized_keys  node2:~/.ssh/authorized_keys

# After deleting the authorized_keys files on node1 and node2, copy the authorized_keys file on node0 to the other two nodes.

In addition to this, it is also a good idea to set up a shared directory so that when files in the shared directory are changed, files in different nodes are also changed, preventing files in different nodes from being out of sync when the model is run on multiple nodes. The shared directory is implemented using nfs-utils and rpcbind.

# Installation of software packages
yum -y install nfs* rpcbind

# Edit the configuration file on the master node
vim /etc/exports
/data/mpi *(rw,sync,no_all_squash,no_subtree_check)

# Start the service on the master node
systemctl start rpcbind
systemctl start nfs

# Mount the directory to be shared on all child nodes node1,node2.
mount node1:/data/mpi/ /data/mpi
mount node2:/data/mpi/ /data/mpi

Distributed launch

Using the Distributed Computing Interface, started by the vqnetrun command, the parameters of vqnetrun are described.

n, np

The vqnetrun interface allows you to control the number of processes started with the -n, -np parameters, as shown in the following example.

Example:

from pyvqnet.distributed import CommController
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")

# vqnetrun -n 2 python test.py
# vqnetrun -np 2 python test.py

H, hosts

The vqnetrun interface allows you to specify nodes and process assignments for cross-node execution via the -H, --hosts interfaces (you must configure the node’s environment successfully to execute in the same environment under the same path when running across nodes), with the following execution example.

Example:

from pyvqnet.distributed import CommController, get_host_name
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")
print(f"LocalRank {Comm_OP.getLocalRank()} hosts name {get_host_name()}")

# vqnetrun -np 4 -H node0:1,node2:1 python test.py
# vqnetrun -np 4 --hosts node0:1,node2:1 python test.py

hostfile, f, hostfile

The vqnetrun interface allows you to specify nodes and process assignments across nodes by specifying a hosts file (when running across nodes, you must configure the node’s environment successfully, executing in the same environment and under the same path), with the command line arguments -hostfile, -f, and --hostfile.

Each line within the file must be formatted as <hostname> slots=<slots> as;

node0 slots=1

node2 slots=1

A sample implementation is as follows

Example:

from pyvqnet.distributed import CommController, get_host_name
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")
print(f"LocalRank {Comm_OP.getLocalRank()} hosts name {get_host_name()}")

# vqnetrun -np 4 -f hosts python test.py
# vqnetrun -np 4 -hostfile hosts python test.py
# vqnetrun -np 4 --hostfile hosts python test.py

output-filename

The vqnetrun interface allows you to save the output to a specified file with the command line parameter --output-filename.

A sample implementation is as follows:

Example:

from pyvqnet.distributed import CommController, get_host_name
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")
print(f"LocalRank {Comm_OP.getLocalRank()} hosts name {get_host_name()}")

# vqnetrun -np 4 --hostfile hosts --output-filename output  python test.py

verbose

The vqnetrun interface can be used with the command line parameter --verbose to instrument inter-node communication and additionally output the results of the instrumentation.

A sample implementation is as follows

Example:

from pyvqnet.distributed import CommController, get_host_name
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")
print(f"LocalRank {Comm_OP.getLocalRank()} hosts name {get_host_name()}")

# vqnetrun -np 4 --hostfile hosts --verbose python test.py

start-timeout

The vqnetrun interface can be used with the command line parameter -start-timeout to specify that all checks are performed and the process is started before the timeout. The default value is 30 seconds.

A sample implementation is as follows

Example:

from pyvqnet.distributed import CommController, get_host_name
Comm_OP = CommController("mpi") # init mpi controller

rank = Comm_OP.getRank()
size = Comm_OP.getSize()
print(f"rank: {rank}, size {size}")
print(f"LocalRank {Comm_OP.getLocalRank()} hosts name {get_host_name()}")

# vqnetrun -np 4 --start-timeout 10 python test.py

h

The vqnetrun interface can output all parameters supported by vqnetrun and a detailed description of the parameters using this flag.

A sample implementation is as follows

# vqnetrun -h

CommController

Distributed computing is used to control the data communication of different processes under cpu and gpu, generate different controllers for cpu (mpi) and gpu (nccl), and call the communication method to complete the communication and synchronization of data between different processes.

__init__

class pyvqnet.distributed.ControlComm.CommController(backend, rank=None, world_size=None)

CommController is used to control the controller of data communication under cpu and gpu, by setting the parameter backend to generate the controller for cpu(mpi) and gpu(nccl). (Currently, the distributed computing function only supports the use of linux operating system system )

参数:

• backend – used to generate the data communication controller for cpu or gpu.

• rank – This parameter is only useful in non-pyvqnet backends, the default value is: None.

• world_size – This parameter is only useful in non-pyvqnet backends, the default value is: None.

返回:

CommController instance.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl") # init nccl controller

# Comm_OP = CommController("mpi") # init mpi controller

getRank()

Used to get the process number of the current process.

返回:

Returns the process number of the current process.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl") # init nccl controller

Comm_OP.getRank()

getSize()

Used to get the total number of processes started.

返回:

Returns the total number of processes.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl") # init nccl controller

Comm_OP.getSize()
# vqnetrun -n 2 python test.py
# 2

getLocalRank()

Used to get the current process number on the current machine.

返回:

The current process number on the current machine.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl") # init nccl controller

Comm_OP.getLocalRank()
# vqnetrun -n 2 python test.py

split_group(rankL)

Divide multiple communication groups according to the process number list set by the input parameter.

参数:

rankL – A list of process group ranks.

返回:

When the backend is nccl, a tuple of process group ranks is returned. When the backend is mpi, returns a list whose length is equal to the number of groups; each element is a tuple (comm, rank), where comm is the MPI communicator of the group and rank is the sequence number within the group..

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

groups = Comm_OP.split_group([[0, 1],[2,3]])
print(groups)
#[[<mpi4py.MPI.Intracomm object at 0x7f53691f3230>, [0, 3]], [<mpi4py.MPI.Intracomm object at 0x7f53691f3010>, [2, 1]]]

barrier()

Synchronization.

返回:

Synchronization.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl")

Comm_OP.barrier()

get_device_num()

Used to get the number of graphics cards on the current node, (only supported on gpu).

返回:

Returns the number of graphics cards on the current node.

Examples:

from pyvqnet.distributed import CommController
Comm_OP = CommController("nccl")

Comm_OP.get_device_num()
# python test.py

allreduce(tensor, c_op='avg')

Supports allreduce communication of data.

参数:

• tensor – Input data.

• c_op – Calculation.

Examples:

from pyvqnet.distributed import CommController
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
print(f"rank {Comm_OP.getRank()}  {num}")

Comm_OP.allreduce(num, "sum")
print(f"rank {Comm_OP.getRank()}  {num}")
# vqnetrun -n 2 python test.py

reduce(tensor, root=0, c_op='avg')

Supports reduce communication of data.

参数:

• tensor – input.

• root – Specifies the node to which the data is returned.

• c_op – Calculation.

Examples:

from pyvqnet.distributed import CommController
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
print(f"rank {Comm_OP.getRank()}  {num}")

Comm_OP.reduce(num, 1)
print(f"rank {Comm_OP.getRank()}  {num}")
# vqnetrun -n 2 python test.py

broadcast(tensor, root=0)

Broadcasts data on the specified process root to all processes.

参数:

• tensor – input.

• root – Specifies node.

Examples:

from pyvqnet.distributed import CommController
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
print(f"rank {Comm_OP.getRank()}  {num}")

Comm_OP.broadcast(num, 1)
print(f"rank {Comm_OP.getRank()}  {num}")
# vqnetrun -n 2 python test.py

allgather(tensor)

Allgather the data on all processes together.

参数:

tensor – input.

Examples:

from pyvqnet.distributed import CommController
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
print(f"rank {Comm_OP.getRank()}  {num}")

num = Comm_OP.allgather(num)
print(f"rank {Comm_OP.getRank()}  {num}")
# vqnetrun -n 2 python test.py

send(tensor, dest)

p2p communication interface.

参数:

• tensor – input.

• dest – Destination process.

Examples:

from pyvqnet.distributed import CommController,get_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
recv = tensor.zeros_like(num)

if get_rank() == 0:
    Comm_OP.send(num, 1)
elif get_rank() == 1:
    Comm_OP.recv(recv, 0)
print(f"rank {Comm_OP.getRank()}  {num}")
print(f"rank {Comm_OP.getRank()}  {recv}")

# vqnetrun -n 2 python test.py

recv(tensor, source)

p2p communication interface.

参数:

• tensor – input.

• source – Acceptance process.

Examples:

from pyvqnet.distributed import CommController,get_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("mpi")

num = tensor.to_tensor(np.random.rand(1, 5))
recv = tensor.zeros_like(num)

if get_rank() == 0:
    Comm_OP.send(num, 1)
elif get_rank() == 1:
    Comm_OP.recv(recv, 0)
print(f"rank {Comm_OP.getRank()}  {num}")
print(f"rank {Comm_OP.getRank()}  {recv}")

# vqnetrun -n 2 python test.py

allreduce_group(tensor, c_op='avg', group=None)

The group allreduce communication interface.

参数:

• tensor – input.

• c_op – Calculation.

• group – Communication group. When using the mpi backend, enter the group generated by init_group or split_group corresponding to the communication group. When using the nccl backend, enter the group number generated by split_group.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("nccl")

groups = Comm_OP.split_group([[0, 1]])

complex_data = tensor.QTensor([3+1j, 2, 1 + get_rank()],dtype=8).reshape((3,1)).toGPU(1000+ get_local_rank())

print(f"allreduce_group before rank {get_rank()}: {complex_data}")

Comm_OP.allreduce_group(complex_data, c_op="sum",group = groups[0])
print(f"allreduce_group after rank {get_rank()}: {complex_data}")
# vqnetrun -n 2 python test.py

reduce_group(tensor, root=0, c_op='avg', group=None)

Intra-group reduce communication interface.

参数:

• tensor – Input.

• root – Specify the process number.

• c_op – Calculation.

• group – Communication group. When using the mpi backend, enter the group generated by init_group or split_group corresponding to the communication group. When using the nccl backend, enter the group number generated by split_group.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("nccl")

groups = Comm_OP.split_group([[0, 1]])

complex_data = tensor.QTensor([3+1j, 2, 1 + get_rank()],dtype=8).reshape((3,1)).toGPU(1000+ get_local_rank())

print(f"reduce_group before rank {get_rank()}: {complex_data}")

Comm_OP.reduce_group(complex_data, c_op="sum",group = groups[0])
print(f"reduce_group after rank {get_rank()}: {complex_data}")
# vqnetrun -n 2 python test.py

broadcast_group(tensor, root=0, group=None)

Intra-group broadcast communication interface.

参数:

• tensor – Input.

• root – Specify the process number to broadcast from, default:0.

• group – Communication group. When using the mpi backend, enter the group generated by init_group or split_group corresponding to the communication group. When using the nccl backend, enter the group number generated by split_group.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("nccl")

groups = Comm_OP.split_group([[0, 1]])

complex_data = tensor.QTensor([3+1j, 2, 1 + get_rank()],dtype=8).reshape((3,1)).toGPU(1000+ get_local_rank())

print(f"broadcast_group before rank {get_rank()}: {complex_data}")

Comm_OP.broadcast_group(complex_data,group = groups[0])
Comm_OP.barrier()
print(f"broadcast_group after rank {get_rank()}: {complex_data}")
# vqnetrun -n 2 python test.py

allgather_group(tensor, group=None)

The group allgather communication interface.

参数:

• tensor – Input.

• group – Communication group. When using the mpi backend, enter the group generated by init_group or split_group corresponding to the communication group. When using the nccl backend, enter the group number generated by split_group.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
import numpy as np
Comm_OP = CommController("nccl")

groups = Comm_OP.split_group([[0, 1]])

complex_data = tensor.QTensor([3+1j, 2, 1 + get_rank()],dtype=8).reshape((3,1)).toGPU(1000+ get_local_rank())

print(f"allgather_group before rank {get_rank()}: {complex_data}")

complex_data = Comm_OP.allgather_group(complex_data,group = groups[0])
print(f"allgather_group after rank {get_rank()}: {complex_data}")
# vqnetrun -n 2 python test.py

grad_allreduce(optimizer)

Update the gradient of the parameters in the optimizer with allreduce.

参数:

optimizer – optimizer.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn.loss import MeanSquaredError
from pyvqnet.optim import Adam
from pyvqnet.nn import activation as F
import numpy as np
Comm_OP = CommController("nccl")

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net().toGPU(1000+ get_local_rank())
opti = Adam(model.parameters(), lr=0.01)
actual = tensor.QTensor([1,1,1,1,1,0,0,0,0,0],dtype=6).reshape((10,1)).toGPU(1000+ get_local_rank())
x = tensor.randn((10, 5)).toGPU(1000+ get_local_rank())
for i in range(10):
    opti.zero_grad()
    model.train()
    result = model(x)
    loss = MeanSquaredError()(actual, result)
    loss.backward()
    # print(f"rank {get_rank()} grad is {model.parameters()[0].grad} para {model.parameters()[0]}")
    Comm_OP.grad_allreduce(opti)
    # print(Comm_OP._allgather(model.parameters()[0]))
    if get_rank() == 0 :
        print(f"rank {get_rank()} grad is {model.parameters()[0].grad} para {model.parameters()[0]} after")
    opti.step()
# vqnetrun -n 2 python test.py

param_allreduce(model)

Update the parameters in the model in an allreduce manner.

参数:

model – Model.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
import numpy as np
Comm_OP = CommController("nccl")

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net().toGPU(1000+ get_local_rank())
print(f"rank {get_rank()} parameters is {model.parameters()}")
Comm_OP.param_allreduce(model)

if get_rank() == 0:
    print(model.parameters())

broadcast_model_params(model, root=0)

Broadcasts the model parameters on the specified process number.

参数:

• model – Models.

• root – Specify the process number.

Examples:

from pyvqnet.distributed import CommController,get_rank,get_local_rank
from pyvqnet.tensor import tensor
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
import numpy as np
Comm_OP = CommController("nccl")

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net().toGPU(1000+ get_local_rank())
print(f"bcast before rank {get_rank()}:{model.parameters()}")
Comm_OP.broadcast_model_params(model, 0)
# model = model
print(f"bcast after rank {get_rank()}: {model.parameters()}")

split_data

In multi-process, use split_data to slice the data according to the number of processes and return the data on the corresponding process.

pyvqnet.distributed.datasplit.split_data(x_train, y_train, shuffle=False)

Set parameters for distributed computation.

param x_train:

np.array - training data.

param y_train:

np.array - Training data labels.

param shuffle:

bool - Whether to shuffle and then slice, default is False.

return:

sliced training data and labels.

Example:

from pyvqnet.distributed import split_data
import numpy as np

x_train = np.random.randint(255, size = (100, 5))
y_train = np.random.randint(2, size = (100, 1))

x_train, y_train= split_data(x_train, y_train)

get_local_rank

Use get_local_rank to get the process number on the current machine.

pyvqnet.distributed.ControlComm.get_local_rank()

Used to get the current process number on the current machine.

返回:

current process number on the current machine.

Example:

from pyvqnet.distributed.ControlComm import get_local_rank

print(get_local_rank())
# vqnetrun -n 2 python test.py

get_rank

Use get_rank to get the process number on the current machine.

pyvqnet.distributed.ControlComm.get_rank()

Used to get the process number of the current process.

返回:

the process number of the current process.

Example:

from pyvqnet.distributed.ControlComm import get_rank

print(get_rank())
# vqnetrun -n 2 python test.py

init_group

Use init_group to initialise cpu-based process groups based on the given list of process numbers.

pyvqnet.distributed.ControlComm.init_group(rank_lists)

Used to initialise the process communication group for mpi backend.

参数:

rank_lists – List of communication process groups.

返回:

A list of initialised process groups.

Example:

from pyvqnet.distributed import *

Comm_OP = CommController("mpi")
num = tensor.to_tensor(np.random.rand(1, 5))
print(f"rank {Comm_OP.getRank()}  {num}")

group_l = init_group([[0,2], [1]])

for comm_ in group_l:
    if Comm_OP.getRank() in comm_[1]:
        Comm_OP.allreduce_group(num, "sum", group = comm_[0])
        print(f"rank {Comm_OP.getRank()}  {num} after")

# vqnetrun -n 3 python test.py

PipelineParallelTrainingWrapper

class pyvqnet.distributed.pp.PipelineParallelTrainingWrapper(args, join_layers, trainset)

Pipeline Parallel Training Wrapper implements 1F1B training. Available only on Linux platforms with a GPU. More algorithm details can be found at (https://www.deepspeed.ai/tutorials/pipeline/).

参数:

• args – Parameter dictionary. See examples.

• join_layers – List of Sequential modules.

• trainset – Dataset.

返回:

PipelineParallelTrainingWrapper instance.

The following uses the CIFAR10 database CIFAR10_Dataset to train the classification task on AlexNet on 2 GPUs. In this example, it is divided into two pipeline parallel processes pipeline_parallel_size = 2. The batch size is train_batch_size = 64, on a single GPU it is train_micro_batch_size_per_gpu = 32. Other configuration parameters can be found in args. In addition, each process needs to configure the environment variable LOCAL_RANK in the __main__ function.

Examples:

import os
import pyvqnet

from pyvqnet.nn import Module,Sequential,CrossEntropyLoss
from pyvqnet.nn import Linear
from pyvqnet.nn import Conv2D
from pyvqnet.nn import activation as F
from pyvqnet.nn import MaxPool2D
from pyvqnet.nn import CrossEntropyLoss

from pyvqnet.tensor import tensor
from pyvqnet.distributed.pp import PipelineParallelTrainingWrapper
from pyvqnet.distributed.configs import comm as dist
from pyvqnet.distributed import *


pipeline_parallel_size = 2

num_steps = 1000

def cifar_trainset_vqnet(local_rank, dl_path='./cifar10-data'):
    transform = pyvqnet.data.TransformCompose([
        pyvqnet.data.TransformResize(256),
        pyvqnet.data.TransformCenterCrop(224),
        pyvqnet.data.TransformToTensor(),
        pyvqnet.data.TransformNormalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
    ])

    trainset = pyvqnet.data.CIFAR10_Dataset(root=dl_path,
                                            mode="train",
                                            transform=transform,layout="HWC")

    return trainset

class Model(Module):
    def __init__(self):
        super(Model, self).__init__()
        self.features = Sequential(
        Conv2D(input_channels=3, output_channels=8, kernel_size=(3, 3), stride=(1, 1), padding='same'),
        F.ReLu(),
        MaxPool2D([2, 2], [2, 2]),

        Conv2D(input_channels=8, output_channels=16, kernel_size=(3, 3), stride=(1, 1), padding='same'),
        F.ReLu(),
        MaxPool2D([2, 2], [2, 2]),

        Conv2D(input_channels=16, output_channels=32, kernel_size=(3, 3), stride=(1, 1), padding='same'),
        F.ReLu(),

        Conv2D(input_channels=32, output_channels=64, kernel_size=(3, 3), stride=(1, 1), padding='same'),
        F.ReLu(),

        Conv2D(input_channels=64, output_channels=64, kernel_size=(3, 3), stride=(1, 1), padding='same'),
        F.ReLu(),
        MaxPool2D([3, 3], [2, 2]),)

        self.cls = Sequential(
        Linear(64 * 27 * 27, 512),
        F.ReLu(),

        Linear(512, 256),
        F.ReLu(),
        Linear(256, 10) )

    def forward(self, x):
        x = self.features(x)
        x = tensor.flatten(x,1)
        x = self.cls(x)

        return x

def join_layers(vision_model):
    layers = [
        *vision_model.features,
        lambda x: tensor.flatten(x, 1),
        *vision_model.cls,
    ]
    return layers


if __name__ == "__main__":


    args = {
    "backend":'nccl',
    "train_batch_size" : 64,
    "train_micro_batch_size_per_gpu" : 32,
    "epochs":5,
"optimizer": {
    "type": "Adam",
    "params": {
    "lr": 0.001
    }},
    "local_rank":dist.get_local_rank(),
    "pipeline_parallel_size":pipeline_parallel_size, "seed":42, "steps":num_steps,
    "loss":CrossEntropyLoss(),
    }
    os.environ["LOCAL_RANK"] = str(dist.get_local_rank())
    trainset = cifar_trainset_vqnet(args["local_rank"])
    w = PipelineParallelTrainingWrapper(args,join_layers(Model()),trainset)

    all_loss = {}

    for i in range(args["epochs"]):
        w.train_batch()

    all_loss = w.loss_dict

ZeroModelInitial

class pyvqnet.distributed.ZeroModelInitial(args, model, optimizer)

Zero1 api interface, currently only for linux platform based on GPU parallel computing.

参数:

• args – parameters dict。

• model – Module。

• optimizer – Optimizer。

返回:

Zero1 Engine.

The following uses the MNIST database to train a classification task on an MLP model on 2 GPUs.

The batch size is train_batch_size = 64, and the stage stage of zero_optimization is set to 1. If Optimizer is None, the setting of optimizer in args is used. Other configuration parameters can be found in args.

In addition, each process needs to be configured with the environment variable LOCAL_RANK.

os.environ["LOCAL_RANK"] = str(dist.get_local_rank())

Examples:

from pyvqnet.distributed import *
from pyvqnet import *
from time import time
import pyvqnet.optim as optim
import pyvqnet.nn as nn
import pyvqnet
import sys
import pyvqnet
import numpy as np
import os
import struct

def load_mnist(dataset="training_data",
            digits=np.arange(2),
            path="./"):
    """
    load mnist data
    """
    from array import array as pyarray
    if dataset == "training_data":
        fname_image = os.path.join(path, "train-images.idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "train-labels.idx1-ubyte").replace(
            "\\", "/")
    elif dataset == "testing_data":
        fname_image = os.path.join(path, "t10k-images.idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "t10k-labels.idx1-ubyte").replace(
            "\\", "/")
    else:
        raise ValueError("dataset must be 'training_data' or 'testing_data'")

    flbl = open(fname_label, "rb")
    _, size = struct.unpack(">II", flbl.read(8))

    lbl = pyarray("b", flbl.read())
    flbl.close()

    fimg = open(fname_image, "rb")
    _, size, rows, cols = struct.unpack(">IIII", fimg.read(16))
    img = pyarray("B", fimg.read())
    fimg.close()

    ind = [k for k in range(size) if lbl[k] in digits]
    num = len(ind)
    images = np.zeros((num, rows, cols),dtype=np.float32)

    labels = np.zeros((num, 1), dtype=int)
    for i in range(len(ind)):
        images[i] = np.array(img[ind[i] * rows * cols:(ind[i] + 1) * rows *
                                cols]).reshape((rows, cols))
        labels[i] = lbl[ind[i]]

    return images, labels


train_images_np, train_labels_np = load_mnist(dataset="training_data", digits=np.arange(10),path="../data/MNIST_data/")
train_images_np = train_images_np / 255.

test_images_np, test_labels_np = load_mnist(dataset="testing_data", digits=np.arange(10),path="../data/MNIST_data/")
test_images_np = test_images_np / 255.

local_rank = pyvqnet.distributed.get_rank()

from pyvqnet.distributed import ZeroModelInitial

class MNISTClassifier(nn.Module):

    def __init__(self):
        super(MNISTClassifier, self).__init__()
        self.fc1 = nn.Linear(28*28, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, 128)
        self.fc4 = nn.Linear(128, 64)
        self.fc5 = nn.Linear(64, 10)
        self.ac = nn.activation.ReLu()

    def forward(self, x:pyvqnet.QTensor):

        x = x.reshape([-1, 28*28])
        x = self.ac(self.fc1(x))
        x = self.fc2(x)
        x = self.fc3(x)
        x = self.fc4(x)
        x = self.fc5(x)
        return x

model = MNISTClassifier()

model.to(local_rank + 1000)

Comm_op = CommController("nccl")
Comm_op.broadcast_model_params(model, 0)

batch_size = 64

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

args_ = {
        "train_batch_size": batch_size,
        "optimizer": {
            "type": "adam",
            "params": {
            "lr": 0.001,
            }
        },
        "zero_optimization": {
            "stage": 1,
        }
    }

os.environ["LOCAL_RANK"] = str(get_local_rank())
model = ZeroModelInitial(args=args_, model=model, optimizer=optimizer)

def compute_acc(outputs, labels, correct, total):
    predicted = pyvqnet.tensor.argmax(outputs, dim=1, keepdims=True)
    total += labels.size
    correct += pyvqnet.tensor.sums(predicted == labels).item()
    return correct, total

train_acc = 0
test_acc = 0
epochs = 5
loss = 0
time1 = time()

for epoch in range(epochs):
    model.train()
    total = 0
    correct = 0
    step = 0

    num_batches = (train_images_np.shape[0] + batch_size - 1) // batch_size

    for i in range(num_batches):

        data_ = tensor.QTensor(train_images_np[i*batch_size: (i+1) * batch_size,:], dtype = kfloat32)
        labels = tensor.QTensor(train_labels_np[i*batch_size: (i+1) * batch_size,:], dtype = kint64)

        data_ = data_.to(local_rank + 1000)
        labels = labels.to(local_rank + 1000)

        outputs = model(data_)
        loss = criterion(labels, outputs)

        model.backward(loss)
        model.step()

        correct, total = compute_acc(outputs, labels, correct, total)
        step += 1
        if step % 50 == 0:
            print(f"Train : rank {get_rank()} Epoch [{epoch+1}/{epochs}], step {step} Loss: {loss.item():.4f} acc {100 * correct / total}")
            sys.stdout.flush()

    train_acc = 100 * correct / total

time2 = time()
print(f'Accuracy of the model on the 10000 Train images: {train_acc}% time cost {time2 - time1}')

ColumnParallelLinear

class pyvqnet.distributed.ColumnParallelLinear(input_size, output_size, weight_initializer, bias_initializer, use_bias, dtype, name, tp_comm)

Tensor-parallel computation with column-parallel linear layer

The linear layer is defined as Y = XA + b. Its 2D parallel rows are A = [A_1, … , A_p].

参数:

• input_size – first dimension of matrix A.

• output_size – second dimension of matrix A.

• weight_initializer – callable - defaults to normal.

• bias_initializer – callable - defaults to zeros.

• use_bias – bool - defaults to True.

• dtype – default: None,use default data type.

• name – name of module,default:””.

• tp_comm – Comm Controller.

The following uses the MNIST database to train a classification task on an MLP model on 2 GPUs.

The usage is similar to that of the classic Linear layer.

Multi-process usage based on vqnetrun -n 2 python test.py.

Examples:

import pyvqnet.distributed
import pyvqnet.optim as optim
import pyvqnet.nn as nn
import pyvqnet
import sys
from pyvqnet.distributed.tensor_parallel import ColumnParallelLinear, RowParallelLinear
from pyvqnet.distributed import *
from time import time

import pyvqnet
import numpy as np
import os
from pyvqnet import *
import pytest

Comm_OP = CommController("nccl")

import struct
def load_mnist(dataset="training_data",
            digits=np.arange(2),
            path="./"):
    """
    load mnist data
    """
    from array import array as pyarray
    # download_mnist(path)
    if dataset == "training_data":
        fname_image = os.path.join(path, "train-images-idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "train-labels-idx1-ubyte").replace(
            "\\", "/")
    elif dataset == "testing_data":
        fname_image = os.path.join(path, "t10k-images-idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "t10k-labels-idx1-ubyte").replace(
            "\\", "/")
    else:
        raise ValueError("dataset must be 'training_data' or 'testing_data'")

    flbl = open(fname_label, "rb")
    _, size = struct.unpack(">II", flbl.read(8))

    lbl = pyarray("b", flbl.read())
    flbl.close()

    fimg = open(fname_image, "rb")
    _, size, rows, cols = struct.unpack(">IIII", fimg.read(16))
    img = pyarray("B", fimg.read())
    fimg.close()

    ind = [k for k in range(size) if lbl[k] in digits]
    num = len(ind)
    images = np.zeros((num, rows, cols),dtype=np.float32)

    labels = np.zeros((num, 1), dtype=int)
    for i in range(len(ind)):
        images[i] = np.array(img[ind[i] * rows * cols:(ind[i] + 1) * rows *
                                cols]).reshape((rows, cols))
        labels[i] = lbl[ind[i]]

    return images, labels

train_images_np, train_labels_np = load_mnist(dataset="training_data", digits=np.arange(10),path="./data/MNIST/raw/")
train_images_np = train_images_np / 255.

test_images_np, test_labels_np = load_mnist(dataset="testing_data", digits=np.arange(10),path="./data/MNIST/raw/")
test_images_np = test_images_np / 255.

local_rank = pyvqnet.distributed.get_rank()

class MNISTClassifier(nn.Module):
    def __init__(self):
        super(MNISTClassifier, self).__init__()
        self.fc1 = RowParallelLinear(28*28, 512, tp_comm = Comm_OP)
        self.fc2 = ColumnParallelLinear(512, 256, tp_comm = Comm_OP)
        self.fc3 = RowParallelLinear(256, 128, tp_comm = Comm_OP)
        self.fc4 = ColumnParallelLinear(128, 64, tp_comm = Comm_OP)
        self.fc5 = RowParallelLinear(64, 10, tp_comm = Comm_OP)
        self.ac = nn.activation.ReLu()

    def forward(self, x:pyvqnet.QTensor):

        x = x.reshape([-1, 28*28])
        x = self.ac(self.fc1(x))
        x = self.fc2(x)
        x = self.fc3(x)
        x = self.fc4(x)
        x = self.fc5(x)
        return x


model = MNISTClassifier()
total_params = sum(p.numel() for p in model.parameters() if p.requires_grad)

model.to(local_rank + 1000)

Comm_OP.broadcast_model_params(model, 0)

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

def compute_acc(outputs, labels, correct, total):
    predicted = pyvqnet.tensor.argmax(outputs, dim=1, keepdims=True)
    total += labels.size
    correct += pyvqnet.tensor.sums(predicted == labels).item()
    return correct, total

train_acc = 0
test_acc = 0
epochs = 5
loss = 0

time1 = time()
for epoch in range(epochs):
    model.train()
    total = 0
    correct = 0
    step = 0

    batch_size = 64
    num_batches = (train_images_np.shape[0] + batch_size - 1) // batch_size

    for i in range(num_batches):
        data_ = tensor.QTensor(train_images_np[i*batch_size: (i+1) * batch_size,:], dtype = kfloat32)
        labels = tensor.QTensor(train_labels_np[i*batch_size: (i+1) * batch_size,:], dtype = kint64)

        data_ = data_.to(local_rank + 1000)
        labels = labels.to(local_rank + 1000)

        optimizer.zero_grad()

        outputs = model(data_)
        loss = criterion(labels, outputs)

        loss.backward()
        optimizer.step()

        correct, total = compute_acc(outputs, labels, correct, total)
        step += 1
        if step % 50 == 0:
            print(f"Train : rank {get_rank()} Epoch [{epoch+1}/{epochs}], step {step} Loss: {loss.item():.4f} acc {100 * correct / total}")
            sys.stdout.flush()

    train_acc = 100 * correct / total
time2 = time()

print(f'Accuracy of the model on the 10000 Train images: {train_acc}% time cost {time2 - time1}')

RowParallelLinear

class pyvqnet.distributed.RowParallelLinear(input_size, output_size, weight_initializer, bias_initializer, use_bias, dtype, name, tp_comm)

Tensor-parallel computation with column-parallel linear layer.

The linear layer is defined as Y = XA + b. A is parallelized along its first dimension and X along its second dimension. A = transpose([A_1 .. A_p]) X = [X_1, …, X_p].

参数:

• input_size – first dimension of matrix A.

• output_size – second dimension of matrix A.

• weight_initializer – callable - defaults to normal.

• bias_initializer – callable - defaults to zeros.

• use_bias – bool - defaults to True.

• dtype – default: None,use default data type.

• name – name of module,default:””.

• tp_comm – Comm Controller.

The following uses the MNIST database to train a classification task on an MLP model on 2 GPUs.

The usage is similar to that of the classic Linear layer.

Multi-process usage based on vqnetrun -n 2 python test.py.

Examples:

import pyvqnet.distributed
import pyvqnet.optim as optim
import pyvqnet.nn as nn
import pyvqnet
import sys
from pyvqnet.distributed.tensor_parallel import ColumnParallelLinear, RowParallelLinear
from pyvqnet.distributed import *
from time import time

import pyvqnet
import numpy as np
import os
from pyvqnet import *
import pytest

Comm_OP = CommController("nccl")

import struct
def load_mnist(dataset="training_data",
            digits=np.arange(2),
            path="./"):
    """
    load mnist data
    """
    from array import array as pyarray
    # download_mnist(path)
    if dataset == "training_data":
        fname_image = os.path.join(path, "train-images-idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "train-labels-idx1-ubyte").replace(
            "\\", "/")
    elif dataset == "testing_data":
        fname_image = os.path.join(path, "t10k-images-idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "t10k-labels-idx1-ubyte").replace(
            "\\", "/")
    else:
        raise ValueError("dataset must be 'training_data' or 'testing_data'")

    flbl = open(fname_label, "rb")
    _, size = struct.unpack(">II", flbl.read(8))

    lbl = pyarray("b", flbl.read())
    flbl.close()

    fimg = open(fname_image, "rb")
    _, size, rows, cols = struct.unpack(">IIII", fimg.read(16))
    img = pyarray("B", fimg.read())
    fimg.close()

    ind = [k for k in range(size) if lbl[k] in digits]
    num = len(ind)
    images = np.zeros((num, rows, cols),dtype=np.float32)

    labels = np.zeros((num, 1), dtype=int)
    for i in range(len(ind)):
        images[i] = np.array(img[ind[i] * rows * cols:(ind[i] + 1) * rows *
                                cols]).reshape((rows, cols))
        labels[i] = lbl[ind[i]]

    return images, labels

train_images_np, train_labels_np = load_mnist(dataset="training_data", digits=np.arange(10),path="./data/MNIST/raw/")
train_images_np = train_images_np / 255.

test_images_np, test_labels_np = load_mnist(dataset="testing_data", digits=np.arange(10),path="./data/MNIST/raw/")
test_images_np = test_images_np / 255.

local_rank = pyvqnet.distributed.get_rank()

class MNISTClassifier(nn.Module):
    def __init__(self):
        super(MNISTClassifier, self).__init__()
        self.fc1 = RowParallelLinear(28*28, 512, tp_comm = Comm_OP)
        self.fc2 = ColumnParallelLinear(512, 256, tp_comm = Comm_OP)
        self.fc3 = RowParallelLinear(256, 128, tp_comm = Comm_OP)
        self.fc4 = ColumnParallelLinear(128, 64, tp_comm = Comm_OP)
        self.fc5 = RowParallelLinear(64, 10, tp_comm = Comm_OP)
        self.ac = nn.activation.ReLu()


    def forward(self, x:pyvqnet.QTensor):

        x = x.reshape([-1, 28*28])
        x = self.ac(self.fc1(x))
        x = self.fc2(x)
        x = self.fc3(x)
        x = self.fc4(x)
        x = self.fc5(x)
        return x

model = MNISTClassifier()
total_params = sum(p.numel() for p in model.parameters() if p.requires_grad)

model.to(local_rank + 1000)
Comm_OP.broadcast_model_params(model, 0)

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

def compute_acc(outputs, labels, correct, total):
    predicted = pyvqnet.tensor.argmax(outputs, dim=1, keepdims=True)
    total += labels.size
    correct += pyvqnet.tensor.sums(predicted == labels).item()
    return correct, total

train_acc = 0
test_acc = 0
epochs = 5
loss = 0

time1 = time()
for epoch in range(epochs):
    model.train()
    total = 0
    correct = 0
    step = 0

    batch_size = 64
    num_batches = (train_images_np.shape[0] + batch_size - 1) // batch_size

    for i in range(num_batches):
        data_ = tensor.QTensor(train_images_np[i*batch_size: (i+1) * batch_size,:], dtype = kfloat32)
        labels = tensor.QTensor(train_labels_np[i*batch_size: (i+1) * batch_size,:], dtype = kint64)

        data_ = data_.to(local_rank + 1000)
        labels = labels.to(local_rank + 1000)

        optimizer.zero_grad()

        outputs = model(data_)
        loss = criterion(labels, outputs)

        loss.backward()
        optimizer.step()

        correct, total = compute_acc(outputs, labels, correct, total)
        step += 1
        if step % 50 == 0:
            print(f"Train : rank {get_rank()} Epoch [{epoch+1}/{epochs}], step {step} Loss: {loss.item():.4f} acc {100 * correct / total}")
            sys.stdout.flush()

    train_acc = 100 * correct / total
time2 = time()

print(f'Accuracy of the model on the 10000 Train images: {train_acc}% time cost {time2 - time1}')

Bit Reordering

Qubit reordering is a technique in bit parallelism. Its core goal is to reduce the number of bit transformations required by bit parallelism by changing the order of quantum logic gates. The following modules are required for building large-bit quantum circuits based on bit parallelism. Refer to the paper Lazy Qubit Reordering for Accelerating Parallel State-Vector-based Quantum Circuit Simulation.

The following interfaces require mpi to launch multiple processes for computation.

DistributeQMachine

class pyvqnet.distributed.qubits_reorder.DistributeQMachine(num_wires, dtype, grad_mode)

A class for simulating bit-parallel variational quantum computations, including quantum states on a subset of bits on each node. Each node applies for a distributed quantum variational circuit simulation via MPI. The value of N must be equal to a power of 2 raised to the number of distributed parallel bits, global_qubit, and can be configured via set_qr_config.

参数:

• num_wires – The number of bits in the complete quantum circuit.

• dtype – The data type of the computation data. The default is pyvqnet.kcomplex64, corresponding to the parameter precision of pyvqnet.kfloat32.

• grad_mode – Set to adjoint when backpropagating DistQuantumLayerAdjoint.

备注

The number of bits input is the number of bits required for the entire quantum circuit. DistributeQMachine will build a quantum simulator based on the global number of bits, which is nums_wires - global_qubit.

Backpropagation must be based on DistQuantumLayerAdjoint.

警告

This interface only supports running under Linux;

The bit-parallel parameters in DistributeQMachine must be configured, as shown in the example, including:

qm.set_just_defined(True)
qm.set_save_op_history_flag(True) # open save op
qm.set_qr_config({'qubit': total qubits number, 'global_qubit':  distributed qubits number})

Examples:

from pyvqnet.distributed import get_rank
from pyvqnet import tensor
from pyvqnet.qnn.vqc import rx, ry, cnot, MeasureAll,rz
import pyvqnet
from pyvqnet.distributed.qubits_reorder import DistributeQMachine,DistQuantumLayerAdjoint
pyvqnet.utils.set_random_seed(123)


qubit = 10
batch_size = 5

class QModel(pyvqnet.nn.Module):
    def __init__(self, num_wires, dtype, grad_mode=""):
        super(QModel, self).__init__()

        self._num_wires = num_wires
        self._dtype = dtype
        self.qm = DistributeQMachine(num_wires, dtype=dtype, grad_mode=grad_mode)

        self.qm.set_just_defined(True)
        self.qm.set_save_op_history_flag(True) # open save op
        self.qm.set_qr_config({"qubit": num_wires, # open qubit reordered, set config
                                "global_qubit": 1}) # global_qubit == log2(nproc)

        self.params = pyvqnet.nn.Parameter([qubit])

        self.measure = MeasureAll(obs={
            "X5":1.0
        })

    def forward(self, x, *args, **kwargs):
        self.qm.reset_states(x.shape[0])

        for i in range(qubit):
            rx(q_machine=self.qm, params=self.params[i], wires=i)
            ry(q_machine=self.qm, params=self.params[3], wires=i)
            rz(q_machine=self.qm, params=self.params[4], wires=i)
        cnot(q_machine=self.qm,  wires=[0, 1])
        rlt = self.measure(q_machine=self.qm)
        return rlt


input_x = tensor.QTensor([[0.1, 0.2, 0.3]], requires_grad=True).toGPU(pyvqnet.DEV_GPU_0+get_rank())

input_x = tensor.broadcast_to(input_x, [2, 3])

input_x.requires_grad = True

quantum_model = QModel(num_wires=qubit,
                    dtype=pyvqnet.kcomplex64,
                    grad_mode="adjoint").toGPU(pyvqnet.DEV_GPU_0+get_rank())

adjoint_model = DistQuantumLayerAdjoint(quantum_model)
adjoint_model.train()

batch_y = adjoint_model(input_x)
batch_y.backward()

print(batch_y)
# mpirun -n 2 python test.py

DistQuantumLayerAdjoint

class pyvqnet.distributed.qubits_reorder.DistQuantumLayerAdjoint(vqc_module, name)

A DistQuantumLayer layer that computes gradients for parameters in bit-parallel computations using the adjoint matrix approach.

参数:

• vqc_module – The input implicit DistributeQMachine module.

• name – The module name.

备注

The input vqc_module module must contain DistributeQMachine. Adjoint backpropagation gradient computations are performed based on DistributeQMachine in bit-parallel computations.

警告

This interface is only supported on Linux;

Examples:

from pyvqnet.distributed import get_rank
from pyvqnet import tensor
from pyvqnet.qnn.vqc import rx, ry, cnot, MeasureAll,rz
import pyvqnet
from pyvqnet.distributed.qubits_reorder import DistributeQMachine,DistQuantumLayerAdjoint
pyvqnet.utils.set_random_seed(123)


qubit = 10
batch_size = 5

class QModel(pyvqnet.nn.Module):
    def __init__(self, num_wires, dtype, grad_mode=""):
        super(QModel, self).__init__()

        self._num_wires = num_wires
        self._dtype = dtype
        self.qm = DistributeQMachine(num_wires, dtype=dtype, grad_mode=grad_mode)

        self.qm.set_just_defined(True)
        self.qm.set_save_op_history_flag(True) # open save op
        self.qm.set_qr_config({"qubit": num_wires, # open qubit reordered, set config
                                    "global_qubit": 1}) # global_qubit == log2(nproc)

        self.params = pyvqnet.nn.Parameter([qubit])

        self.measure = MeasureAll(obs={
            "X5":1.0
        })

    def forward(self, x, *args, **kwargs):
        self.qm.reset_states(x.shape[0])

        for i in range(qubit):
            rx(q_machine=self.qm, params=self.params[i], wires=i)
            ry(q_machine=self.qm, params=self.params[3], wires=i)
            rz(q_machine=self.qm, params=self.params[4], wires=i)
        cnot(q_machine=self.qm,  wires=[0, 1])
        rlt = self.measure(q_machine=self.qm)
        return rlt


input_x = tensor.QTensor([[0.1, 0.2, 0.3]], requires_grad=True).toGPU(pyvqnet.DEV_GPU_0+get_rank())

input_x = tensor.broadcast_to(input_x, [2, 3])

input_x.requires_grad = True

quantum_model = QModel(num_wires=qubit,
                    dtype=pyvqnet.kcomplex64,
                    grad_mode="adjoint").toGPU(pyvqnet.DEV_GPU_0+get_rank())

adjoint_model = DistQuantumLayerAdjoint(quantum_model)
adjoint_model.train()

batch_y = adjoint_model(input_x)
batch_y.backward()

print(batch_y)
# mpirun -n 2 python test.py