Prev Tutorial: Quantum Circuit and Quantum Program
Next Tutorial: Quantum Intermediate Compiler
Introduction
Quantum state encoding is the process of converting classical information into quantum states. In the process of solving classical problems using quantum algorithms, quantum state encoding is a crucial step. For example, when using the HHL algorithm to solve the following linear system of equations.
$$\begin{aligned} \begin{aligned} A=\left(\begin{array}{cc} 1 & -1 / 3 \ -1 / 3 & 1 \end{array}\right), \vec{x}=\left(\begin{array}{l} x_{1} \ x_{2} \end{array}\right), \vec{b}=\left(\begin{array}{l} 1 \ 0 \end{array}\right) \end{aligned} \end{aligned}$$
To encode the vector b into the quantum circuit, most quantum state encoding methods prepare states based on the \(\left|0\right\rangle\) basis state. The classical information after encoding is represented in various parameters of the quantum circuit.
In this tutorial, we will discuss four quantum encoding methods, including basis encoding, angle encoding, amplitude encoding, and IQP encoding. In pyqpanda3, these four encoding methods are built into the Encode class.
The Encode class provides various quantum state encoding methods to encode quantum states into different formats. These include basis encoding, which encodes quantum states as binary strings; angle encoding, which encodes information into angles and phases; and multiple amplitude encoding methods, including those for sparse and dense data, as well as approximate amplitude encoding.
Basis Encoding
Basis encoding [1] converts an n-bit binary string x into a quantum state of an n-qubit system:
\(\left|x\right\rangle=\left|\psi\right\rangle\) where \(\left|\psi\right\rangle\) is the computational basis state after conversion.
For example, encoding the 4-bit binary string 1001 results in the quantum state: \(|1001\rangle\)
Example Usage:
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
x = '1001'
qubits = range(4)
cir_encode=Encode()
cir_encode.basic_encode(qubits,x)
prog = QProg()
prog << cir_encode.get_circuit()
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
{'0000': 0.0, '0001': 0.0, '0010': 0.0, '0011': 0.0, '0100': 0.0, '0101': 0.0, '0110': 0.0, '0111': 0.0, '1000': 0.0, '1001': 1.0, '1010': 0.0, '1011': 0.0, '1100': 0.0, '1101': 0.0, '1110': 0.0, '1111': 0.0}
Angle Encoding
Angle encoding [1] encodes classical information using the rotation angles of quantum gates such as \((R_x)\), \((R_y)\), and \((R_z)\).
$$\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{N} \cos \left(x_{i}\right)|0\rangle+\sin \left(x_{i}\right)|1\rangle \end{aligned}$$
where \((|x\rangle)\) represents the classical data vector to be encoded.
Below, we use the \((R_y)\) gate to encode a set of angles [\pi, \pi] as an example.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
x = [np.pi,np.pi]
qubits = range(2)
cir_encode=Encode()
cir_encode.angle_encode(qubits,x)
prog = QProg()
prog << cir_encode.get_circuit()
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
{'00': 1.405799628556214e-65, '01': 3.749399456654644e-33, '10': 3.749399456654644e-33, '11': 1.0}
Since a single qubit can encode both angle and phase information, it is possible to encode a classical data vector of length N onto \(\lceil N \rceil\) qubits.
$$\begin{aligned} |\boldsymbol{x}\rangle=\bigotimes_{i=1}^{\lceil N / 2\rceil} \cos \left(\pi x_{2 i-1}\right)|0\rangle+e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle \end{aligned}$$
In this representation, two data points are encoded separately into the rotation angle \(\cos \left(\pi x_{2 i-1}\right)|0\rangle\) and the phase information \(e^{2 \pi i x_{2 i}} \sin \left(\pi x_{2 i-1}\right)|1\rangle\).
It can be observed that in classical angle encoding, the classical data vector \(x\) is rotated around the \(y-axis\) by \(\pi\). Since dense angle encoding encodes half of the information into the phase of the quantum state, we can call the run interface to obtain the quantum state information of the system.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
x = [np.pi,np.pi]
qubits = range(1)
cir_encode=Encode()
cir_encode.dense_angle_encode(qubits,x)
prog = QProg()
prog << cir_encode.get_circuit()
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
{'0': 3.749399456654644e-33, '1': 1.0}
Amplitude Encoding
Amplitude encoding maps a data vector of length \(N\) onto the amplitudes of \(\lceil log_{2}N \rceil\) qubits. The mathematical representation is as follows:
$$\begin{aligned} \left|\psi\right\rangle=x_{0}|0\rangle+\cdots+x_{N-1}|N-1\rangle \end{aligned}$$
However, since the trace of a quantum system in either a pure or mixed state must be 1, the data needs to be normalized. Therefore, input validation is performed during the encoding process.
A quantum state encoding algorithm typically considers three key factors:
- Circuit depth
- Circuit width (number of qubits)
- Number of CNOT gates
To accommodate these factors, pyqpanda3 provides different encoding methods. Additionally, depending on the data structure, the encoding can be categorized into dense data encoding and sparse data encoding.
The Top-down encoding [2] method first processes the data vector to generate an angle tree and then encodes the data sequentially from the root node downward, as illustrated below:
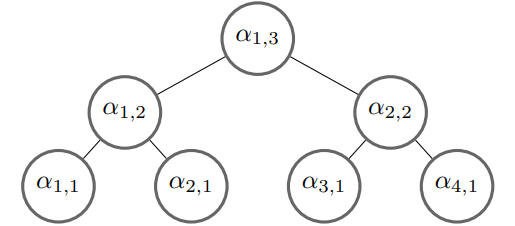
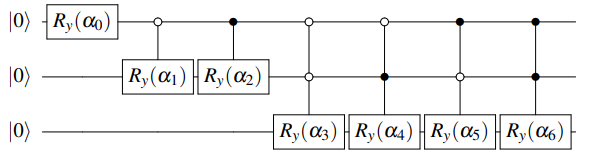
This encoding approach requires a circuit width of \(O(\lceil log_{2} N \rceil)\) and a circuit depth of \(O(n)\).
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(3)
cir_encode=Encode()
cir_encode.amplitude_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌──────────────┐ ┌──────────────┐ ┌──────────────┐ >
q_0: |0>───────────────── ──────────────── ─── ──────────────── ─── ┤RY(0.00000000)├ ─── ┤RY(3.14159265)├ ─── ┤RY(0.00000000)├ >
┌──────────────┐ ┌──────────────┐ └───────┬──────┘ ┌─┐ └───────┬──────┘ ┌─┐ └───────┬──────┘ >
q_1: |0>───────────────── ┤RY(1.57079633)├ ─── ┤RY(0.00000000)├ ─── ────────*─────── ┤X├ ────────*─────── ┤X├ ────────*─────── >
┌──────────────┐ └───────┬──────┘ ┌─┐ └───────┬──────┘ ┌─┐ │ └─┘ │ ├─┤ │ >
q_2: |0>─┤RY(1.91063324)├ ────────*─────── ┤X├ ────────*─────── ┤X├ ────────*─────── ─── ────────*─────── ┤X├ ────────*─────── >
└──────────────┘ └─┘ └─┘ └─┘ >
c : / ═
┌──────────────┐
q_0: |0>─── ┤RY(3.14159265)├ ───
┌─┐ └───────┬──────┘ ┌─┐
q_1: |0>┤X├ ────────*─────── ┤X├
└─┘ │ ├─┤
q_2: |0>─── ────────*─────── ┤X├
└─┘
c : /
{'000': 1.2497998188848808e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}
In contrast to the Top-down encoding method, the Bottom-top encoding [2] approach constructs a quantum circuit with a width of \(O(n)\) and a depth of \(O(\lceil log_{2} N \rceil)\).
In this method, the leftmost subtree of the angle tree (including \(\alpha_{0}\) , \(\alpha_{1}\) and \(\alpha_{3}\) corresponds to output qubits, while the remaining qubits serve as ancillary qubits. The construction process is illustrated below:
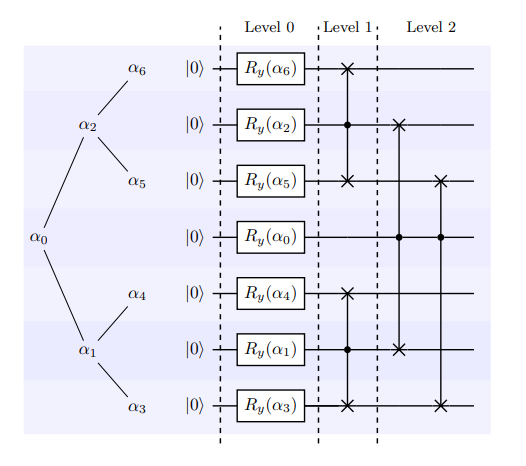
In this structure, level 1 and level 2 apply controlled-SWAP (CSWAP) gates, which are responsible for exchanging the quantum states between ancillary qubits and output qubits.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(7)
cir_encode=Encode()
cir_encode.dc_amplitude_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌──────────────┐
q_0: |0>─┤RY(1.91063324)├ ──── *─ *─
├──────────────┤ │ │
q_1: |0>─┤RY(0.00000000)├ ──*─ X─ ┼─
├──────────────┤ │ │ │
q_2: |0>─┤RY(1.57079633)├ *─┼─ X─ ┼─
├──────────────┤ │ │ │
q_3: |0>─┤RY(3.14159265)├ ┼─X─ ── X─
├──────────────┤ │ │ │
q_4: |0>─┤RY(0.00000000)├ ┼─X─ ── ┼─
├──────────────┤ │ │
q_5: |0>─┤RY(3.14159265)├ X─── ── X─
├──────────────┤ │
q_6: |0>─┤RY(0.00000000)├ X─── ── ──
└──────────────┘
c : / ═
{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848817e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}
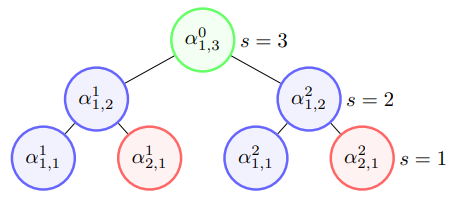
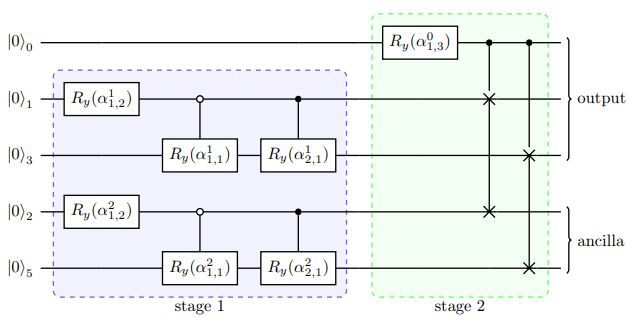
The Bidirectional Amplitude Encoding [2] method combines both Top-down and Bottom-top encoding approaches. It introduces a parameter \(split\) that allows control over the circuit depth and width.
The circuit width is given by:
\(O_{w}\left(2^{split}+\log _{2}^{2}(N)-split^{2}\right)\) The circuit depth is given by:
\(O_{d}\left((split+1) \frac{N}{2^{split}}\right)\) In pyqpanda3, the default value for \(split\) is \(n/2\).
From the formulas for **(O_{w})** and **(O_{d})**, we can observe that:
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(5)
cir_encode=Encode()
cir_encode.bid_amplitude_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌──────────────┐
q_0: |0>─┤RY(1.91063324)├ ──────────────── ─── ──────────────── ─── *─ *─
├──────────────┤ ┌─┐ ┌─┐ │ │
q_1: |0>─┤RY(0.00000000)├ ────────*─────── ┤X├ ────────*─────── ┤X├ X─ ┼─
└──────────────┘ ┌───────┴──────┐ └─┘ ┌───────┴──────┐ └─┘ │ │
q_2: |0>───────────────── ┤RY(0.00000000)├ ─── ┤RY(3.14159265)├ ─── ┼─ X─
┌──────────────┐ └──────────────┘ ┌─┐ └──────────────┘ ┌─┐ │ │
q_3: |0>─┤RY(1.57079633)├ ────────*─────── ┤X├ ────────*─────── ┤X├ X─ ┼─
└──────────────┘ ┌───────┴──────┐ └─┘ ┌───────┴──────┐ └─┘ │
q_4: |0>───────────────── ┤RY(0.00000000)├ ─── ┤RY(3.14159265)├ ─── ── X─
└──────────────┘ └──────────────┘
c : / ═
{'000': 1.2497998188848807e-33, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 1.2497998188848813e-33, '101': 0.3333333333333334, '110': 0.3333333333333334, '111': 0.0}
As shown in Top-down Amplitude Encoding, encoding a classical dataset of length \(N\) using \(\lceil log_{2} N \rceil\) qubits requires approximately \(2^{2n}\) controlled rotation gates. This significantly reduces the fidelity of the quantum circuit. However, Schmidt Decomposition-Based Amplitude Encoding [3] can effectively reduce the number of controlled rotation gates in the circuit.
A pure quantum state \(|\psi\rangle\) can be expressed as follows:
$$\begin{aligned} |\psi\rangle=\sum_{i=1}^{k} \lambda_{i}\left|\alpha_{i}\right\rangle \otimes\left|\beta_{i}\right\rangle \end{aligned}$$
Further, it can be rewritten as:
$$\begin{aligned} |\psi\rangle=\sum_{i=1}^{k} \lambda_{i}\left|\alpha_{i}\right\rangle \otimes\left|\beta_{i}\right\rangle \end{aligned}$$
where \(\left|e_{i}\right\rangle \in \mathbb{C}^{m},\left|f_{j}\right\rangle \in \mathbb{C}^{n}\). The matrix \(C\) can undergo Singular Value Decomposition (SVD):
\(C=U \Sigma V^{\dagger}\)
From the above equations, we derive:
\(\sigma_{i i}=\lambda_{i}\)
\(\left|\alpha_{i}\right\rangle=U\left|e_{i}\right\rangle\)
\(\left|\beta_{i}\right\rangle=V^{\dagger}\left|f_{i}\right\rangle\)
where \(\sigma_{i i}\) represents the singular values of \(C\). The corresponding circuit construction is shown below.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(3)
cir_encode=Encode()
cir_encode.schmidt_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌────┐ ┌───────────────────────────────────────────────────┐ >
q_0: |0>─────────────────────────────────────────────────────── ┤CNOT├ ┤U4(0.00000000, 1.57079633, 2.12437069, -3.14159265)├ >
┌────────────────────────────────────────────────────┐ └──┬─┘ └───────────────────────────────────────────────────┘ >
q_1: |0>─┤U4(-0.00000000, 3.14159265, 0.00000000, -3.14159265)├ ───┼── ───────────────────────────────────────────────────── >
├──────────────┬─────────────────────────────────────┘ │ ┌───────────────────────────────────────────────────┐ >
q_2: |0>─┤RY(0.72972766)├────────────────────────────────────── ───*── ┤U4(1.57079633, 0.00000000, 2.03444394, -3.14159265)├ >
└──────────────┘ └───────────────────────────────────────────────────┘ >
c : / ═
┌────────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐
q_0: |0>──*─ ┤U4(-0.00000000, -0.00000000, 2.12437069, 4.71238898)├ ──*─ ┤U4(-0.00000000, 0.46364761, 0.00000000, 1.10714872)├─
┌─┴┐ ├──────────────────────────────────────────────────┬─┘ ┌─┴┐ ├───────────────────────────────────────────────────┴┐
q_1: |0>┤CZ├ ┤U4(0.00000000, 0.00000000, 1.57079633, 1.57079633)├── ┤CZ├ ┤U4(0.78539816, -1.57079633, 1.57079633, -6.28318531)├
└──┘ └──────────────────────────────────────────────────┘ └──┘ └────────────────────────────────────────────────────┘
q_2: |0>──── ────────────────────────────────────────────────────── ──── ──────────────────────────────────────────────────────
c : /
{'000': 3.51862174721677e-32, '001': 0.33333333333333315, '010': 4.8452179519763874e-32, '011': 3.505620428081208e-33, '100': 1.025086436597375e-31, '101': 0.3333333333333338, '110': 0.3333333333333329, '111': 2.723201269651864e-32}
MPS Approximation Encoding [4] is an algorithm that uses a low-rank matrix product state (MPS) to approximate a distribution. This method allows the distribution to be expressed with fewer CNOT gates, and the expression is in a nearest-neighbor form, making it directly applicable to the chip. The reduction in the number of two-qubit gates also helps increase the success rate of the distribution preparation. The quantum circuit diagram is shown below:
It can be seen that this function supports various data types (double, complex), where layers refers to the number of layers used for the matrix product state approximation, and sweeps refers to the number of iterations through which the environment tensor is optimized. The mathematical expression for the environment tensor is as follows:
$$\begin{aligned} \hat{\mathcal{F}}_m=\operatorname{Tr}_{\bar{U}_m}\left[\prod_{i=M}^{m+1} U_i\left|\psi_{\chi_{\max }}\right\rangle\left\langle 0^{\otimes N}\right| \prod_{j=1}^{m-1} U_j^{\dagger}\right] \end{aligned}$$
Where \(\operatorname{Tr}_{\bar{U}_m}\) denotes the partial trace over the qubits that do not interact with \(U_m\), and the environment tensor \(\hat{\mathcal{F}}_m\) is represented as a 4x4 matrix. In practice, this can be calculated by removing \(U_m\) from the quantum circuit and contracting the remaining tensors (see below), while always maintaining the MPS structure.
Finally, to adapt the preparation algorithm to the chip's topology, the \(chi\) parameter is set to 2.
As an example, we use the W-state to demonstrate the magic of MPS approximation encoding. Regardless of the number of qubits in the W-state, the encoding can be done accurately with a single layer of disentanglement. Therefore, for data with low entanglement, such as Gaussian distribution data, it can be approximated at a lower depth.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(3)
cir_encode=Encode()
cir_encode.approx_mps_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌───────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐ >
q_0: |0>─┤U4(-0.00000000, 1.57079633, 0.14422034, 3.14159265)├─ ──*─ ┤U4(0.00000000, -3.14159265, 3.02600465, 1.57079633)├─ >
├──────────────────────────────────────────────────┬┘ ┌─┴┐ ├───────────────────────────────────────────────────┴┐ >
q_1: |0>─┤U4(0.00000000, 1.57079633, 2.52929625, 0.00000000)├── ┤CZ├ ┤U4(-0.00000000, 3.14159265, 0.93069872, -1.57079633)├ >
├──────────────────────────────────────────────────┴─┐ └──┘ └────────────────────────────────────────────────────┘ >
q_2: |0>─┤U4(0.00000000, -1.57079633, 2.62654637, -3.14159265)├ ──── ────────────────────────────────────────────────────── >
└────────────────────────────────────────────────────┘ >
c : / ═
┌──────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐ >
q_0: |0>──*─ ┤U4(0.00000000, 0.00000000, 2.74728685, 0.00000000)├── ┤U4(-0.00000000, 2.44026625, 1.57079633, 1.57079633)├ >
┌─┴┐ ├──────────────────────────────────────────────────┴─┐ ├───────────────────────────────────────────────────┤ >
q_1: |0>┤CZ├ ┤U4(-0.00000000, 3.14159265, 1.60338538, -3.14159265)├ ┤U4(0.00000000, 4.71238898, 1.16262513, -0.00000000)├ >
└──┘ └────────────────────────────────────────────────────┘ └───────────────────────────────────────────────────┘ >
q_2: |0>──── ────────────────────────────────────────────────────── ───────────────────────────────────────────────────── >
>
c : /
>
q_0: |0>──── ───────────────────────────────────────────────────── ──── ────────────────────────────────────────────────────── >
┌───────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐ >
q_1: |0>──*─ ┤U4(0.00000000, -3.14159265, 1.77399044, 1.57079633)├ ──*─ ┤U4(0.00000000, -3.14159265, 1.51402457, 3.14159265)├─ >
┌─┴┐ ├───────────────────────────────────────────────────┤ ┌─┴┐ ├───────────────────────────────────────────────────┴┐ >
q_2: |0>┤CZ├ ┤U4(0.00000000, 3.14159265, 1.39084874, -1.57079633)├ ┤CZ├ ┤U4(-0.00000000, -3.14159265, 1.24134660, 3.14159265)├ >
└──┘ └───────────────────────────────────────────────────┘ └──┘ └────────────────────────────────────────────────────┘ >
c : /
┌───────────────────────────────────────────────────┐ >
q_0: |0>─────────────────────────────────────────────────────── ──*─ ┤U4(0.00000000, -3.14159265, 3.09540078, 1.57079633)├ >
┌─────────────────────────────────────────────────────┐ ┌─┴┐ ├───────────────────────────────────────────────────┤ >
q_1: |0>┤U4(-0.00000000, -3.32978396, 1.57079633, -1.57079633)├ ┤CZ├ ┤U4(0.00000000, 3.14159265, 0.31160284, -1.57079633)├ >
├───────────────────────────────────────────────────┬─┘ └──┘ └───────────────────────────────────────────────────┘ >
q_2: |0>┤U4(0.00000000, -0.41642121, 1.57079633, 1.57079633)├── ──── ───────────────────────────────────────────────────── >
└───────────────────────────────────────────────────┘ >
c : /
┌───────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐ >
q_0: |0>──*─ ┤U4(-0.00000000, 4.71238898, 1.57079633, 1.08485200)├ ┤U4(0.00000000, 1.57079633, 1.03964616, -3.14159265)├ >
┌─┴┐ ├───────────────────────────────────────────────────┤ ├───────────────────────────────────────────────────┤ >
q_1: |0>┤CZ├ ┤U4(1.57079633, -1.57079633, 1.57079633, 1.76216405)├ ┤U4(0.00000000, 0.00000000, 1.85661223, -0.00000000)├ >
└──┘ └───────────────────────────────────────────────────┘ └───────────────────────────────────────────────────┘ >
q_2: |0>──── ───────────────────────────────────────────────────── ───────────────────────────────────────────────────── >
>
c : /
>
q_0: |0>──── ─────────────────────────────────────────────────────── ──── ────────────────────────────────────────────────────── >
┌───────────────────────────────────────────────────┐ ┌────────────────────────────────────────────────────┐ >
q_1: |0>──*─ ┤U4(0.00000000, -1.57079633, 0.13083119, 4.71238898)├── ──*─ ┤U4(-0.00000000, 3.14159265, 0.04863628, -1.57079633)├ >
┌─┴┐ ├───────────────────────────────────────────────────┴─┐ ┌─┴┐ ├───────────────────────────────────────────────────┬┘ >
q_2: |0>┤CZ├ ┤U4(-0.00000000, -0.00000000, 1.57079633, -0.00000000)├ ┤CZ├ ┤U4(0.00000000, -1.57079633, 1.57079633, 3.14159265)├─ >
└──┘ └─────────────────────────────────────────────────────┘ └──┘ └───────────────────────────────────────────────────┘ >
c : /
>
q_0: |0>──── ────────────────────────────────────────────────────── ─────────────────────────────────────────────────────── >
┌────────────────────────────────────────────────────┐ ┌─────────────────────────────────────────────────────┐ >
q_1: |0>──*─ ┤U4(0.00000000, -0.00000000, 2.38474385, -4.71238898)├ ┤U4(-0.00000000, -0.00000000, 0.41015532, -3.14159265)├ >
┌─┴┐ ├───────────────────────────────────────────────────┬┘ ├────────────────────────────────────────────────────┬┘ >
q_2: |0>┤CZ├ ┤U4(1.57079633, -7.85398163, 1.57079633, 1.05132326)├─ ┤U4(-0.00000000, 0.00000000, 2.83411843, -3.14159265)├─ >
└──┘ └───────────────────────────────────────────────────┘ └────────────────────────────────────────────────────┘ >
c : /
┌───────────────────────────────────────────────────┐ ┌───────────────────────────────────────────────────┐ >
q_0: |0>──*─ ┤U4(0.00000000, -1.57079633, 0.23969156, 4.71238898)├── ──*─ ┤U4(0.00000000, -0.00000000, 0.05916140, 1.57079633)├ >
┌─┴┐ ├───────────────────────────────────────────────────┴─┐ ┌─┴┐ ├───────────────────────────────────────────────────┤ >
q_1: |0>┤CZ├ ┤U4(-0.00000000, -0.00000000, 1.57079633, -0.00000000)├ ┤CZ├ ┤U4(0.00000000, -1.57079633, 1.57079633, 3.14159265)├ >
└──┘ └─────────────────────────────────────────────────────┘ └──┘ └───────────────────────────────────────────────────┘ >
q_2: |0>──── ─────────────────────────────────────────────────────── ──── ───────────────────────────────────────────────────── >
>
c : /
┌───────────────────────────────────────────────────┐ >
q_0: |0>──*─ ┤U4(0.00000000, 3.14159265, 0.91540970, -3.14159265)├─ ───────────────────────────────────────────────────── >
┌─┴┐ ├───────────────────────────────────────────────────┴┐ ┌───────────────────────────────────────────────────┐ >
q_1: |0>┤CZ├ ┤U4(1.57079633, -3.14159265, 2.89220717, -1.57079633)├ ┤U4(0.00000000, 4.71238898, 1.09507112, -0.00000000)├ >
└──┘ └────────────────────────────────────────────────────┘ └───────────────────────────────────────────────────┘ >
q_2: |0>──── ────────────────────────────────────────────────────── ───────────────────────────────────────────────────── >
>
c : /
q_0: |0>──── ─────────────────────────────────────────────────────── ──── ────────────────────────────────────────────────────── ──── ──────────────────────────────────────────────────────
┌───────────────────────────────────────────────────┐ ┌────────────────────────────────────────────────────┐ ┌────────────────────────────────────────────────────┐
q_1: |0>──*─ ┤U4(0.00000000, -1.57079633, 0.24153608, 4.71238898)├── ──*─ ┤U4(-0.00000000, 3.14159265, 0.13122312, -1.57079633)├ ──*─ ┤U4(0.00000000, -3.14159265, 0.62086323, -0.00000000)├
┌─┴┐ ├───────────────────────────────────────────────────┴─┐ ┌─┴┐ ├───────────────────────────────────────────────────┬┘ ┌─┴┐ ├───────────────────────────────────────────────────┬┘
q_2: |0>┤CZ├ ┤U4(-0.00000000, -0.00000000, 1.57079633, -0.00000000)├ ┤CZ├ ┤U4(0.00000000, -1.57079633, 1.57079633, 3.14159265)├─ ┤CZ├ ┤U4(1.57079633, -3.14159265, 1.13824884, 1.57079633)├─
└──┘ └─────────────────────────────────────────────────────┘ └──┘ └───────────────────────────────────────────────────┘ └──┘ └───────────────────────────────────────────────────┘
c : /
{'000': 1.8649098631244054e-31, '001': 0.3333333333333338, '010': 6.214926642473421e-31, '011': 3.0992622541939764e-31, '100': 7.662665571759249e-31, '101': 0.3333333333333339, '110': 0.33333333333333254, '111': 1.1994732202454884e-30}
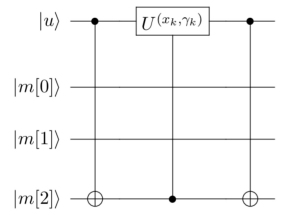
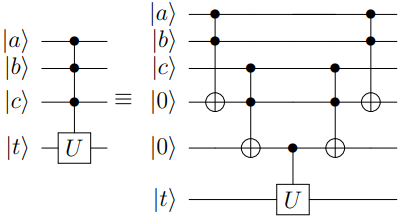
Double Sparse Quantum State Encoding [5] constructs the quantum circuit using \(n\) auxiliary qubits. Let's take encoding \(|001\rangle\) as an example, as shown in the figure below:
Here, \(|\mu\rangle\) is the auxiliary register used to apply rotation gates, controlled by the output register \(|m\rangle\). When the number of 1s in the index of the character to be encoded is large, multiple controlled gates are required. To reduce the number of multi-controlled gates in the circuit, we add a few auxiliary registers and use Toffoli gates for decomposition. The principle of this method is shown in the following diagram:
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(6)
cir_encode=Encode()
cir_encode.ds_quantum_state_preparation(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌─┐ ┌───────────────────────────────────────┐ ┌───────────────────────────────────────┐ >
q_0: |0>─┤X├ ───*── ┤U3(-1.23095942, 0.00000000, 0.00000000)├ ───*── ───*── ───*── ─── ┤U3(-1.57079633, 0.00000000, 0.00000000)├ >
└─┘ │ └───────────────────┬───────────────────┘ │ │ │ ┌─┐ └───────────────────┬───────────────────┘ >
q_2: |0>──── ───┼── ────────────────────┼──────────────────── ───┼── ───┼── ───┼── ┤X├ ────────────────────*──────────────────── >
┌──┴─┐ │ ┌──┴─┐ ┌──┴─┐ │ └┬┘ >
q_3: |0>──── ┤CNOT├ ────────────────────*──────────────────── ┤CNOT├ ┤CNOT├ ───┼── ─*─ ───────────────────────────────────────── >
└────┘ └────┘ └────┘ │ │ >
q_4: |0>──── ────── ───────────────────────────────────────── ────── ────── ───┼── ─┼─ ───────────────────────────────────────── >
┌──┴─┐ │ >
q_5: |0>──── ────── ───────────────────────────────────────── ────── ────── ┤CNOT├ ─*─ ───────────────────────────────────────── >
└────┘ >
c : / ═
┌───────────────────────────────────────┐
q_0: |0>─── ───*── ───*── ───*── ───*── ─── ┤U3(-3.14159265, 0.00000000, 0.00000000)├ ───
┌─┐ │ │ │ │ ┌─┐ └───────────────────┬───────────────────┘ ┌─┐
q_2: |0>┤X├ ───┼── ───┼── ───┼── ───┼── ┤X├ ────────────────────*──────────────────── ┤X├
└┬┘ ┌──┴─┐ │ │ │ └┬┘ └┬┘
q_3: |0>─*─ ┤CNOT├ ───┼── ───┼── ───┼── ─┼─ ───────────────────────────────────────── ─┼─
│ └────┘ │ ┌──┴─┐ │ │ │
q_4: |0>─┼─ ────── ───┼── ┤CNOT├ ───┼── ─*─ ───────────────────────────────────────── ─*─
│ ┌──┴─┐ └────┘ ┌──┴─┐ │ │
q_5: |0>─*─ ────── ┤CNOT├ ────── ┤CNOT├ ─*─ ───────────────────────────────────────── ─*─
└────┘ └────┘
c : /
{'000': 0.0, '001': 0.3333333333333334, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333333, '110': 0.33333333333333315, '111': 0.0}
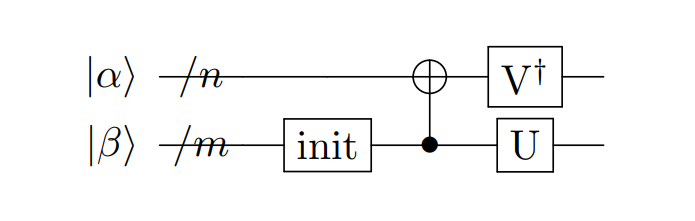
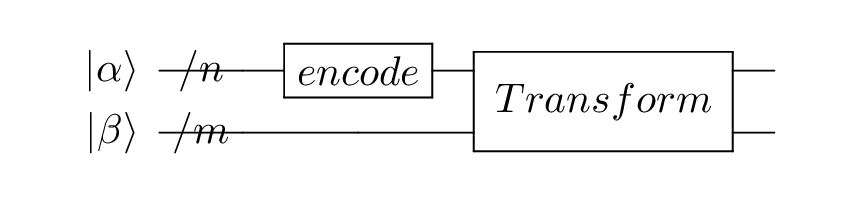
Sparse Isometry Encoding [6] is different from double sparse quantum state encoding in that it does not require auxiliary qubits to construct the circuit. The sparse_isometry encoding first encodes the non-zero elements \(x\) of a sparse data vector of length \(N\) into the first \(\lceil log_2len(x) \rceil\) quantum bits, and then applies controlled-X gates to transform them. The circuit construction is shown in the figure below:
Here, \(n+m=\lceil log_2N \rceil\) \(|\alpha\rangle\) is the encoding module for the \(\lceil log_2len(x) \rceil\) non-zero elements, and \(|\beta\rangle\) represents the remaining qubits. The transform module is the transformation module.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(3)
cir_encode=Encode()
cir_encode.sparse_isometry(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
python
┌──────────────┐ ┌──────────────┐ ┌─┐ ┌─┐ ┌─┐ ┌─┐ ┌─┐ ┌─┐
q_0: |0>───────────────── ┤RY(0.00000000)├ ─── ┤RY(1.57079633)├ ┤X├ ─*─ ┤X├ ┤X├ ┤X├ ─*─ ┤X├ ┤X├
┌──────────────┐ └───────┬──────┘ ┌─┐ └───────┬──────┘ ├─┤ │ ├─┤ └┬┘ └─┘ │ ├─┤ └┬┘
q_1: |0>─┤RY(1.23095942)├ ────────*─────── ┤X├ ────────*─────── ┤X├ ─*─ ┤X├ ─┼─ ─── ─*─ ┤X├ ─┼─
└──────────────┘ └─┘ └─┘ ┌┴┐ └─┘ │ ┌┴┐ └─┘ │
q_2: |0>───────────────── ──────────────── ─── ──────────────── ─── ┤X├ ─── ─*─ ─── ┤X├ ─── ─*─
└─┘ └─┘
c : / ═
{'000': 0.0, '001': 0.3333333333333333, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.33333333333333315, '110': 0.3333333333333334, '111': 0.0}
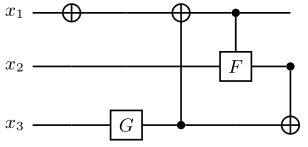
Polynomial Sparse Quantum State Encoding [7] is a sparse data encoding method in which the number of non-zero elements in a sparse data vector is linearly related to the number of qubits. The circuit encoding depth is \(O\left(|S|^{2} \log (|S|) n\right)\), where \(|S|\) is the number of non-zero elements, and \(n\) is the required number of qubits, which is \(\lceil log_2N \rceil\), with \(N\) being the length of the sparse data. Below is an example of encoding \(|x\rangle=1/\sqrt{3}(|001\rangle+|100\rangle+|111\rangle)\), with the circuit construction shown as follows:
Here, the F gate maps \(|0\rangle\) to \(1/\sqrt{3}|0\rangle+1/\sqrt{3}|1\rangle\), while the G gate maps \(|0\rangle\) to \(1/\sqrt{3}|0\rangle+2/\sqrt{3}|1\rangle\).
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [0,1/np.sqrt(3),0,0,0,1/np.sqrt(3),1/np.sqrt(3),0]
data = np.asarray(data)
qubits = range(3)
cir_encode=Encode()
cir_encode.efficient_sparse(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌─┐ ┌────┐ ┌────┐
q_0: |0>─┤X├ ──────────────────────────────────────── ┤CNOT├ ────── ──────────────────────────────────────── ┤CNOT├ ────── ───
└─┘ └──┬─┘ ┌────┐ └──┬─┘ ┌────┐
q_1: |0>──── ──────────────────────────────────────── ───┼── ┤CNOT├ ────────────────────*─────────────────── ───┼── ┤CNOT├ ───
┌─┐ ┌──────────────────────────────────────┐ │ └──┬─┘ ┌───────────────────┴──────────────────┐ │ └──┬─┘ ┌─┐
q_2: |0>─┤X├ ┤U3(1.23095942, 0.00000000, 0.00000000)├ ───*── ───*── ┤U3(1.57079633, 0.00000000, 0.00000000)├ ───*── ───*── ┤X├
└─┘ └──────────────────────────────────────┘ └──────────────────────────────────────┘ └─┘
c : / ═
{'000': 0.0, '001': 0.33333333333333315, '010': 0.0, '011': 0.0, '100': 0.0, '101': 0.3333333333333334, '110': 0.3333333333333333, '111': 0.0}
IQP Encoding
IQP Encoding [8] is an encoding method applied in quantum machine learning. It encodes classical data x into:
$$\begin{aligned} |\mathbf{x}\rangle=\left(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\right)^{\boldsymbol{r}}\left|0^{n}\right\rangle \end{aligned}$$
where \(r\) represents the depth of the quantum circuit, i.e., the number of times \(\mathrm{U}_{\mathrm{Z}}(\mathbf{x}) \mathrm{H}^{\otimes n}\) is repeated. \(\mathrm{H}^{\otimes n}\) is a layer of Hadamard gates acting on all qubits. The operator \(\mathrm{U}_\mathrm{Z}\) is defined as:
$$\begin{aligned} \mathrm{U}_\mathrm{Z}(\mathbf{x})=\prod_{[i, j] \in S} R_{Z_{i} Z_{j}}\left(x_{i} x_{j}\right) \bigotimes_{k=1}^{n} R_{z}\left(x_{k}\right) \end{aligned}$$
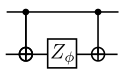
Here, \(S\)is a set, and for each pair of qubits in this set, we apply the \(R_{ZZ}\) gate to them. The construction of the \(R_{ZZ}\) gate is shown below:
Next, we introduce the encoding for data = [-1.3, 1.8, 2.6, -0.15] as an example.
import numpy as np
if __name__=="__main__":
qvm = CPUQVM()
data = [-1.3, 1.8, 2.6, -0.15]
data = np.asarray(data)
qubits = range(4)
cir_encode=Encode()
cir_encode.iqp_encode(qubits,data)
prog = QProg()
prog << cir_encode.get_circuit()
print(prog)
encode_qubits = cir_encode.get_out_qubits()
qvm.run(prog,1)
result = qvm.result().get_prob_dict(encode_qubits)
print(result)
┌─┐ ┌───────────────┐
q_0: |0>─┤H├ ┤RZ(-1.30000000)├ ───*── ───────────────── ───*── ────── ──────────────── ────── ────── ───────────────── ──────
├─┤ ├──────────────┬┘ ┌──┴─┐ ┌───────────────┐ ┌──┴─┐
q_1: |0>─┤H├ ┤RZ(1.80000000)├─ ┤CNOT├ ┤RZ(-2.34000000)├ ┤CNOT├ ───*── ──────────────── ───*── ────── ───────────────── ──────
├─┤ ├──────────────┤ └────┘ └───────────────┘ └────┘ ┌──┴─┐ ┌──────────────┐ ┌──┴─┐
q_2: |0>─┤H├ ┤RZ(2.60000000)├─ ────── ───────────────── ────── ┤CNOT├ ┤RZ(4.68000000)├ ┤CNOT├ ───*── ───────────────── ───*──
├─┤ ├──────────────┴┐ └────┘ └──────────────┘ └────┘ ┌──┴─┐ ┌───────────────┐ ┌──┴─┐
q_3: |0>─┤H├ ┤RZ(-0.15000000)├ ────── ───────────────── ────── ────── ──────────────── ────── ┤CNOT├ ┤RZ(-0.39000000)├ ┤CNOT├
└─┘ └───────────────┘ └────┘ └───────────────┘ └────┘
c : / ═
{'0000': 0.06250000000000001, '0001': 0.06250000000000001, '0010': 0.06250000000000004, '0011': 0.06249999999999999, '0100': 0.06250000000000001, '0101': 0.06250000000000003, '0110': 0.06250000000000001, '0111': 0.06250000000000001, '1000': 0.06250000000000001, '1001': 0.0625, '1010': 0.06250000000000003, '1011': 0.0625, '1100': 0.0625, '1101': 0.06250000000000004, '1110': 0.06250000000000001, '1111': 0.06250000000000003}
References
[1] Schuld, Maria. "Quantum machine learning models are kernel methods."[J] arXiv:2101.11020 (2021).
[2] Araujo I F, Park D K, Ludermir T B, et al. "Configurable sublinear circuits for quantum state preparation."[J]. arXiv preprint arXiv:2108.10182, 2021.
[3] Ghosh K. "Encoding classical data into a quantum computer"[J]. arXiv preprint arXiv:2107.09155, 2021.
[4] Rudolph M S, Chen J, Miller J, et al. Decomposition of matrix product states into shallow quantum circuits[J]. arXiv preprint arXiv:2209.00595, 2022.
[5] de Veras T M L, da Silva L D, da Silva A J. "Double sparse quantum state preparation"[J]. arXiv preprint arXiv:2108.13527, 2021.
[6] Malvetti E, Iten R, Colbeck R. "Quantum circuits for sparse isometries"[J]. Quantum, 2021, 5: 412.
[7] N. Gleinig and T. Hoefler, "An Efficient Algorithm for Sparse Quantum State Preparation," 2021 58th ACM/IEEE Design Automation Conference (DAC), 2021, pp. 433-438, doi: 10.1109/DAC18074.2021.9586240.
[8] Havlíček, Vojtěch, et al. "Supervised learning with quantum-enhanced feature spaces." Nature 567.7747 (2019): 209-212.