Basic Concepts

Variational Quantum Algorithm

Variational Quantum Algorithm(VQA) provides a general framework that can be used to solve a wide range of problems. For an optimization problem, the loss function is defined by the expected value of the observable state generated by a parameterized quantum circuit, and then a classical optimizer is used to optimize the parameters. The Quantum Approximate Optimization Algorithm (QAOA) and the Variational Quantum Eigensolver (VQE) are classic application examples.

A QAOA Example

Parameterized Quantum Circuit

The unitary matrix of the parameterized quantum circuit is \( U\left ( \theta \right ) \)。Among them, \( \theta \) is a variable parameter, and \( U\left ( \theta \right ) \) is determined by the actual value of \( \theta \) and the composition of each quantum gate in the parameterized quantum circuit.（Prepare Parameterized Quantum Circuits Using QPanda3）

Parameterized Quantum State

The parameterized quantum state is obtained by applying a variational quantum circuit to an initial state.（Obtain the parameterized quantum state after applying given parameter values using QPanda3）： \(|\psi(\theta)\rangle=U(\theta)|0\rangle^{{ }^{\otimes n}} \)

The Hamiltonian Expectation in Variational Quantum Algorithms

The Hamiltonian expectation corresponding to the quantum state \( \left | \psi \right \rangle \) and the Hamiltonian operator \( H \) is defined as： \( \langle H\rangle=\langle\psi| H|\psi\rangle \)
The Hamiltonian expectation corresponding to the parameterized quantum state \(\left | \psi \left ( \theta \right ) \right \rangle \) and the Hamiltonian operator \( H \) is： \( \left \langle H \right \rangle = \left \langle \psi\left ( \theta \right ) \right | H \left | \psi \left ( \theta \right ) \right \rangle \)
The Hamiltonian expectation corresponding to the variational quantum circuit \( U\left ( \theta \right ) \) and the Hamiltonian operator \( H \) is（Calculate the Hamiltonian expectation value using QPanda3）： \( \left \langle H \right \rangle = \left \langle 0 \right | ^{\otimes n}U^{\dagger }\left ( \theta \right ) HU\left ( \theta \right ) \left | 0 \right \rangle ^{\otimes n}\)

Gradient Computation in Variational Quantum Algorithms

Here, the concept of gradient is described in vector form (without restricting the gradient to be expressed only in vector form).：

The gradient is a vector of partial derivatives of the objective function \( \left \langle H \right \rangle \) (here, the Hamiltonian expectation) with respect to the parameters \( \theta \) (described here in vector form), where m is the number of parameters.（Calculate the gradient values using QPanda3）： \( \nabla \left \langle H \right \rangle = \left ( \frac{\nabla \left \langle H\right \rangle }{\partial \theta_{1} },\frac{\nabla \left \langle H\right \rangle }{\partial \theta_{2} },\dots ,\frac{\nabla \left \langle H\right \rangle }{\partial \theta_{m} } \right ) \)

Basic Usage Methods

API Doc of VQCircuit

General Usage Procedure

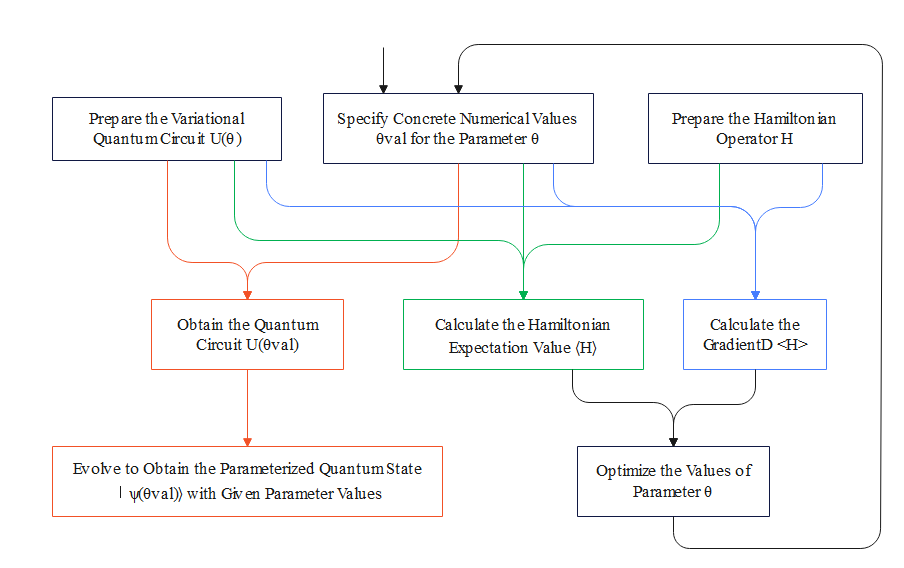
Prepare a Parameterized Quantum Circuit

Procedure Steps

Sequence	Step	QPanda3 Interface
1	Define the format of parameter \( \theta \)	set_Param interface
2	Design the structure of the variational quantum circuit \( U\left ( \theta \right ) \)	using the << operator and append interface

API DOC

Example Code

from pyqpanda3.vqcircuit import VQCircuit
from pyqpanda3.core import QCircuit,X,RX,RY,Y
 
def get_vqc1():
  vqc = VQCircuit()
  vqc.set_Param([2]) # 1> Define parameter θ as a one-dimensional vector with a length of 2. 2> Parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits.
  p0 = vqc.Param([0],'p0') # Assign the name p0 to θ_0
  p1 = vqc.Param([1],'p1') # Assign the name p1 to θ_1
  e = 3.14*p0*p1+p1+4 #An expression composed of the elements of parameter θ (supporting mixed operations of addition, multiplication, and scalar multiplication)
  vqc << X(0) #Add X gate to the variational quantum circuit U(θ)
  vqc << RX(0,3.14) #Add the RX gate to the variational quantum circuit U(θ), with a fixed parameter of 3.14
  vqc << RY(0,e) # Add RY gate to the variational quantum circuit U(θ), where the parameters of the gate are variable and consist of expressions formed by the elements of parameter θ
  return vqc
def get_vqc2():
  vqc2 = VQCircuit()
  vqc2.set_Param([3])
  P0 = vqc2.Param([0],'P0')
  P1 = vqc2.Param([1],'P1')
  P2 = vqc2.Param([2],'P2')
  cir = QCircuit()
  cir << Y(0)
  vqc2 << cir # Add all quantum logic gates from the QCircuit object to the variational quantum circuit U(θ)
  vqc1 = get_vqc1() # For clarity, the parameter θ corresponding to vqc1 is referred to as θ1, and the parameter θ corresponding to vqc2 is referred to as θ2. The two elements of θ1 are θ1[0] and θ1[1], with their respective names being p0 and p1. The three elements of θ2 are θ2[0], θ2[1], and θ2[2], with their respective names being P0, P1, and P2.
  vqc2.append(vqc1, [(vqc1.Param([0]), vqc2.Param([0])), (vqc1.Param([1]), vqc2.Param([1]))]) # Reuse the structure of vqc1. For the parameter θ, θ1[0] will be replaced with θ2[0], and θ1[1] will be replaced with θ2[1].
  return vqc2
 
vqc1 = get_vqc1()
print('vqc1:')
vqc1.display_ansatz() # Print the structure of the variational quantum circuit
print()
vqc2 = get_vqc2()
print('vqc2:')
vqc2.display_ansatz()

Output result of the example code

vqc1:
X q[0]
RX q[0],(3.14000000)
RY q[0],(((3.14*p0*p1+p1)+4))
 
vqc2:
Y q[0]
X q[0]
RX q[0],(3.14000000)
RY q[0],(((3.14*P0*P1+P1)+4))

Note

The form of parameter θ is not limited to a vector form.
The structure of the variational quantum circuit here is presented in a form similar to OriginIR.
QPanda3 also supports evaluating expressions
QPanda3 supports obtaining the total number of elements in parameter θ

Obtain The Parameterized Quantum State After Applying Given Parameter Values

Target

The variational quantum circuit \( U\left ( \theta \right ) \) and the actual numerical values \( \theta val \) for the parameters \( \theta \) have been prepared. Obtain \( \left | \psi\left ( \theta val \right ) \right \rangle \).

Example Code

from pyqpanda3.vqcircuit import VQCircuit
from pyqpanda3.core import QCircuit,X,RX,RY,Y,CPUQVM,QProg
def get_vqc():
    # Prepare the variational quantum circuit U(θ)
    vqc = VQCircuit()
    vqc.set_Param([2])  # 1> Agree that the parameter θ is a one-dimensional vector with a length of 2, 2> The parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits
    vqc << RX(0, vqc.Param([0]))  # Add a parameterized quantum gate RX, whose parameter corresponds to the first element of the vector θ
    vqc << RY(1, vqc.Param([1]))
    return vqc
def get_param_val():
    # Prepare the actual numerical values θval for the parameter θ
    param_val = [5.14, 6.14]  # The number of elements should be consistent with the number of elements in the parameter θ (vector)
    return param_val
 
def get_qstate(vqc, param_val):
    # Obtain ∣ψ(θval)⟩
    cir = vqc(param_val).at([0])  # Obtain U(θval)
    qvm = CPUQVM()
    qvm.run(QProg(cir), 1)  # Perform the evolution
    stv = qvm.result().get_state_vector()
    return stv
 
vqc = get_vqc()  # Prepare the variational quantum circuit U(θ)
param_val = get_param_val()  # Prepare the actual numerical values θval for the parameter θ
stv = get_qstate(vqc, param_val)  # Obtain ∣ψ(θval)⟩
print('∣ψ(θval)⟩:',stv)

Output result of the example code

∣ψ(θval)⟩: [(0.8388860014815892+0j), 0.5395864336991233j, (-0.06016089509492038+0j), -0.03869656040878351j]

Calculate The Hamiltonian Expectation Value

Target

The variational quantum circuit \( U\left ( \theta \right ) \), the actual numerical values \( \theta val \) for the parameter \( \theta \), and the Hamiltonian operator \( H \) have been prepared. Calculate the Hamiltonian expectation value \( \left \langle H \right \rangle \) .

API DOC

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
from pyqpanda3.core import QCircuit,X,RX,RY,Y,CPUQVM,QProg
from pyqpanda3.hamiltonian import Hamiltonian
def get_vqc():
    # Prepare the variational quantum circuit U(θ)
    vqc = VQCircuit()
    vqc.set_Param([2])  # 1> Agree that the parameter θ is a one-dimensional vector with a length of 2. 2> The parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits.
    vqc << RX(0, vqc.Param([0]))  # Add a parameterized quantum gate RX, whose parameter corresponds to the first element of the vector θ
    vqc << RY(1, vqc.Param([1]))
    return vqc
 
def get_param_val():
    # Prepare the actual numerical values θval for the parameter θ
    param_val = [2.14, 3.14]  # The number of elements should be consistent with the number of elements in the parameter θ (vector)
    return param_val
 
def get_hamiltonian():
    # Prepare the Hamiltonian operator H
    paulis = [
        ('YY', [0, 1], (12.36525580995888 + 14.85172018664403j)),  # (Pauli basis, qubit indices on which the Pauli basis acts, coefficient)
        ('YX', [0, 1], (12.920260765526914 + 26.29613065236354j))  # The qubit indices used should be consistent with those used in the quantum circuit
    ]
 
    return Hamiltonian(paulis)
  
def get_hamiltonian_expectation(vqc, param_val, ham):
    # Obtain the Hamiltonian expectation value (Method 1)
    res = vqc(param_val).expval_hamiltonian(ham, [0], used_threads=4, backend='CPU')
    return res
 
def get_hamiltonian_expectation2(vqc: VQCircuit, param_val, ham):
    # Obtain the Hamiltonian expectation value (Method 2)
    # The interface get_gradients_and_expectation can obtain both the gradient values and the expectation values simultaneously. Here, only the expectation value is returned.
    res = vqc.get_gradients_and_expectation(params=param_val, observable=ham, diff_method=DiffMethod.ADJOINT_DIFF).expectation_val()
    return res
 
vqc = get_vqc()  # Prepare the variational quantum circuit U(θ)
param_val = get_param_val()  # Prepare the actual numerical values θval for the parameter θ
ham = get_hamiltonian()  # It is recommended not to use 'H' as the variable name to avoid naming conflicts with the H gate.
ham_expectation = get_hamiltonian_expectation(vqc, param_val, ham)  # Obtain the Hamiltonian expectation value (Method 1)
ham_expectation2 = get_hamiltonian_expectation2(vqc, param_val, ham)  # Obtain the Hamiltonian expectation value (Method 2)
 
print('ham_expectation:',ham_expectation)
print('ham_expectation2:',ham_expectation2)

Output result of the example code

ham_expectation: -0.01733304686759475

ham_expectation2: -0.01733304686759475

Calculate The Gradient Values

Target

The variational quantum circuit \( U\left ( \theta \right ) \), the actual numerical values \( \theta val \) for the parameter \( \theta \), and the Hamiltonian operator \( H \) have been prepared. Now, calculate the gradient values.

API DOC

Note: The parameterized quantum gates currently supported by QPanda3 for gradient computation include RX, RY, RZ, CRX, CRY, and CRZ.

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
from pyqpanda3.core import QCircuit,X,RX,RY,Y,CPUQVM,QProg
from pyqpanda3.hamiltonian import Hamiltonian
 
def get_vqc():
    # Prepare the variational quantum circuit U(θ)
    vqc = VQCircuit()
    vqc.set_Param([2])  # 1> Agree that the parameter θ is a one-dimensional vector with a length of 2. 2> The parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits.
    vqc << RX(0, vqc.Param([0]))  # Add a parameterized quantum gate RX, whose parameter corresponds to the first element of the vector θ
    vqc << RY(1, vqc.Param([1]))
    return vqc
 
def get_param_val():
    # Prepare the actual numerical values θval for the parameter θ
    param_val = [2.14, 3.14]  # The number of elements should be consistent with the number of elements in the parameter θ (vector)
    return param_val
 
def get_hamiltonian():
    # Prepare the Hamiltonian operator H
    paulis = [
        ('YY', [0, 1], (12.36525580995888 + 14.85172018664403j)),  # (Pauli basis, qubit indices on which the Pauli basis acts, coefficient)
        ('YX', [0, 1], (12.920260765526914 + 26.29613065236354j))  # The qubit indices used should be consistent with those used in the quantum circuit
    ]
 
    return Hamiltonian(paulis)
 
def get_gradient(vqc, param_val, ham):
    # Obtain the gradient values (Method 1)
    return vqc.get_gradients(params=param_val, observable=ham, diff_method=DiffMethod.ADJOINT_DIFF)
 
def get_gradient2(vqc: VQCircuit, param_val, ham):
    # Obtain the gradient values (Method 2)
    # The interface get_gradients_and_expectation can obtain both the gradient values and the expectation values simultaneously.
    return vqc.get_gradients_and_expectation(params=param_val, observable=ham, diff_method=DiffMethod.ADJOINT_DIFF)
 
vqc = get_vqc()  # Prepare the variational quantum circuit U(θ)
param_val = get_param_val()  # Prepare the actual numerical values θval for the parameter θ
ham = get_hamiltonian()  # It is recommended not to use 'H' as the variable name to avoid naming conflicts with the H gate.
res1 = get_gradient(vqc, param_val, ham)  # Obtain the gradient values (Method 1)
res2 = get_gradient2(vqc, param_val, ham)  # Obtain the gradient values (Method 2)
 
print('res1:',res1)
print('res1 gradient:',res1.gradients())
print('res2:',res2)
print('res2 gradient:',res2.gradients())

Output result of the example code

res1: {gradient(double):{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}}
res1 gradient: [0.011090474368968659, 23.39317090007428]
res2: (gradient and expectation){"expectation":-0.017333,"gradients":{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}}
res2 gradient: [0.011090474368968659, 23.39317090007428]

Note

QPanda3 supports obtaining the total number of elements in the parameter θ

Other Usage Methods

Parameter θ In The Form Of A Matrix Or Tensor

Corresponds to a 2D array or a multi-dimensional array in programming languages.

API DOC

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
from pyqpanda3.core import QCircuit,X,RX,RY,Y,CPUQVM,QProg,RZ
from pyqpanda3.hamiltonian import Hamiltonian
 
def get_vqc():
    # Prepare the variational quantum circuit U(θ)
    vqc = VQCircuit()
    vqc.set_Param([2, 2, 2])  # 1> Agree that the parameter θ is a 3D tensor with a shape of (2, 2, 2). 2> The parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits.
    vqc << RX(0, vqc.Param([0, 0, 0], 'P000'))  # Add a parameterized quantum gate RX, whose parameter corresponds to the 0th element of the tensor θ
    vqc << RY(0, vqc.Param([0, 0, 1], 'P001'))  # The parameter of this gate corresponds to the 1st element of the tensor θ
    vqc << RZ(1, vqc.Param([0, 1, 0], 'P010'))  # The parameter of this gate corresponds to the 2nd element of the tensor θ
    vqc << RY(1, vqc.Param([0, 1, 1], 'P011'))  # The parameter of this gate corresponds to the 3rd element of the tensor θ
    vqc << RX(0, vqc.Param([1, 0, 0], 'P100'))  # The parameter of this gate corresponds to the 4th element of the tensor θ
    vqc << RY(0, vqc.Param([1, 0, 1], 'P101'))  # The parameter of this gate corresponds to the 5th element of the tensor θ
    vqc << RZ(1, vqc.Param([1, 1, 0], 'P110'))  # The parameter of this gate corresponds to the 6th element of the tensor θ
    vqc << RY(1, vqc.Param([1, 1, 1], 'P111'))  # The parameter of this gate corresponds to the 7th element of the tensor θ
    return vqc
 
def get_param_val():
    # Prepare the actual numerical values θval for the parameter θ
    param_val = [
        [
            [2.00, 3.01],
            [4.10, 5.11]
        ],
        [
            [20.00, 30.01],
            [40.10, 50.11]
        ]
        # The number of elements should be consistent with the number of elements in the parameter θ (tensor)
    ]
    return param_val
 
def get_hamiltonian():
    # Prepare the Hamiltonian operator H
    paulis = [
        ('YY', [0, 1], (12.36525580995888 + 14.85172018664403j)),  # (Pauli basis, qubit indices on which the Pauli basis acts, coefficient)
        ('YX', [0, 1], (12.920260765526914 + 26.29613065236354j))  # The qubit indices used should be consistent with those used in the quantum circuit
    ]
 
    return Hamiltonian(paulis)
 
def get_cir(vqc, param_val):
    # Obtain |ψ(θval)⟩
    return vqc(param_val).at([0])  # Obtain U(θval)
 
def get_expectation_and_gradient(vqc: VQCircuit, param_val, ham):
    # Obtain the gradient values (Method 2)
    # The interface get_gradients_and_expectation can obtain both the gradient values and the expectation values simultaneously.
    return vqc.get_gradients_and_expectation(params=param_val, observable=ham, diff_method=DiffMethod.ADJOINT_DIFF)
 
vqc = get_vqc()  # Prepare the variational quantum circuit U(θ)
param_val = get_param_val()  # Prepare the actual numerical values θval for the parameter θ
ham = get_hamiltonian()  # It is recommended not to use 'H' as the variable name to avoid naming conflicts with the H gate.
res = get_expectation_and_gradient(vqc, param_val, ham)  # Obtain the gradient values (Method 2)
 
print('vqc:')
vqc.display_ansatz()
print('\ncir ir:\n',get_cir(vqc,param_val).originir())
print('res:',res)
print('res gradient:',res.gradients())
print('res hamiltonian expectation:',res.expectation_val())

Output result of the example code

UserWarning: VQCircuit.get_gradients_and_expectation : The input parameter A is not a one-dimensional array.
The elements of A will be processed in row-major order.
  return vqc.get_gradients_and_expectation(params=param_val,observable=ham,diff_method=DiffMethod.ADJOINT_DIFF)
vqc:
RX q[0],(P000)
RY q[0],(P001)
RZ q[1],(P010)
RY q[1],(P011)
RX q[0],(P100)
RY q[0],(P101)
RZ q[1],(P110)
RY q[1],(P111)
 
cir ir:
 QINIT 2
CREG 1
RX q[0],(2.00000000)
RY q[0],(3.01000000)
RZ q[1],(4.10000000)
RY q[1],(5.11000000)
RX q[0],(20.00000000)
RY q[0],(30.01000000)
RZ q[1],(40.10000000)
RY q[1],(50.11000000)
 
res: (gradient and expectation){"expectation":-0.162402,"gradients":{Parameter.at([0]):-0.963576,Parameter.at([1]):-2.8101,Parameter.at([2]):5.12893,Parameter.at([3]):-19.6122,Parameter.at([4]):0.143741,Parameter.at([5]):-6.85959,Parameter.at([6]):-15.2735,Parameter.at([7]):6.39117}}
res gradient: [-0.9635762918972298, -2.8101035948737088, 5.128933515832114, -19.612201408718036, 0.14374054299616468, -6.859590953208836, -15.273535159436635, 6.3911729646014805]
res hamiltonian expectation: -0.16240194962603027

Note

For matrices (2D arrays) or tensors (multi-dimensional arrays), QPanda3 processes the internal data in row-major order. If values like [0,1,2,3,4,5], [[0,1],[2,3],[4,5]], and [[0,1,2],[3,4,5]] are used as the value of θ, QPanda3 will print a warning message, process them in the same manner, and obtain the same results. The warning message is intended to remind users to ensure the reasonableness of the dimensional information of the arrays.
The structure of the variational quantum circuit here is presented in a form similar to OriginIR.

Determination Of The Number Of Elements In The Parameter θ

The total number of elements in the parameter \( \theta \) should remain consistent with the data format set using set_Param.
The product of the elements in the vector passed to set_Param is the total number of elements in the parameter \( \theta \).
QPanda3 provides an interface called mutable_parameter_total to obtain the total number of elements in the parameter \( \theta \).

API DOC

mutable_parameter_total

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
vqc = VQCircuit()
vqc.set_Param([3,4,5])
res = vqc.mutable_parameter_total()
print('res:',res)

Output result of the example code

res: 60

Expression Evaluation

Supported operations: addition, multiplication, and scalar multiplication

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
 
vqc = VQCircuit()
 
def prepare_theta():
    # Prepare the parameter vector θ and the elements that make up the expression
    vqc.set_Param([3])  # Set the parameter θ as a one-dimensional vector with 3 elements
    a = vqc.Param([0], 'a')
    b = vqc.Param([1], 'b')
    c = vqc.Param([2], 'c')
    return a, b, c
 
def get_expression(a, b, c):
    # Prepare an expression composed of the elements of the vector θ
    return 3.14 * a * b + c + 4.14
 
def update_param_vals():
    # Assign values to the parameter vector θ
    param_val = [5, 6, 7]
    vqc(param_val)  # Using either the interface that generates a QCircuit object or the interface that calculates gradients can complete the assignment of values to the vector θ
 
def get_expression_val():
    # Obtain the value of the expression
    d.calculate_expression_val()  # Calculate the value
    return d.get_expression_val()  # Return the value
 
a, b, c = prepare_theta()  # Prepare the parameter vector θ and the elements that make up the expression
d = get_expression(a, b, c)  # Prepare an expression composed of the elements of the vector θ
update_param_vals()  # Assign values to the parameter vector θ
d_val = get_expression_val()  # Obtain the value of the expression
 
print('d:',d)
print('val of d:',d_val)

Output result of the example code

d: ((3.14*a*b+c)+4.14)

val of d: 105.34

Other Interfaces For Gradient Calculation And Hamiltonian Expectation Value Calculation

Serial Number	Interface	Description	API
1	def get_gradients(self, params: numpy.ndarray[numpy.float64], observable, diff_method: DiffMethod)	Given a set of numerical values for the parameter vector \( \theta \), calculate the gradient values corresponding to this set of parameter values and a Hamiltonian expectation value	DOC
2	def get_gradients(self, params: numpy.ndarray[numpy.float64], observable, param_group_total: int, diff_method: DiffMethod)	Given param_group_total sets of numerical values for the parameter vector \( \theta \), calculate param_group_total sets of gradient values corresponding to these parameter value sets	DOC
3	def get_gradients_and_expectation(self, params: numpy.ndarray[numpy.float64], observable, diff_method: DiffMethod)	Given a set of numerical values for the parameter vector \( \theta \), compute a corresponding set of gradient values and a Hamiltonian expectation value for this set of parameter values	DOC
4	def get_gradients_and_expectation(self, params: numpy.ndarray[numpy.float64], observable, param_group_total: int, diff_method: DiffMethod)	Given param_group_total sets of numerical values for the parameter vector \( \theta \), compute param_group_total sets of gradient values and param_group_total Hamiltonian expectation values corresponding to these sets of parameter values	DOC

Example Code

from pyqpanda3.vqcircuit import VQCircuit,DiffMethod
from pyqpanda3.core import QCircuit,X,RX,RY,Y,CPUQVM,QProg
from pyqpanda3.hamiltonian import Hamiltonian
 
def get_vqc():
    # Prepare the variational quantum circuit U(θ)
    vqc = VQCircuit()
    vqc.set_Param([2])  # 1> Agree that the parameter θ is a one-dimensional vector of length 2, 2> The parameter θ is bound to the variational quantum circuit U(θ) and cannot be used for other variational quantum circuits
    vqc << RX(0, vqc.Param([0]))  # Add a parameterized quantum gate RX, whose parameter corresponds to the first element of the vector θ
    vqc << RY(1, vqc.Param([1]))
    return vqc
 
def get_hamiltonian():
    # Prepare the Hamiltonian operator H
    paulis = [
        ('YY', [0, 1], (12.36525580995888 + 14.85172018664403j)),  # (Pauli basis, qubit indices on which the Pauli basis acts, coefficient)
        ('YX', [0, 1], (12.920260765526914 + 26.29613065236354j))  # The qubit indices used should be consistent with those used in the quantum circuit
    ]
    return Hamiltonian(paulis)
 
def fun1(vqc, ham):
    param_val = [2.14, 3.14]
    pq3_res1 = vqc.get_gradients(param_val, ham, DiffMethod.ADJOINT_DIFF)
    print('pq3_res1:', pq3_res1)
    print('pq3_res1.gradients():', pq3_res1.gradients())  # Returns a one-dimensional array as a list, storing the gradient values corresponding to all elements of θ
    print()
 
def fun2(vqc, ham):
    param_val = [2.14, 3.14, 4.14, 5.14]  # Or [[2.14, 3.14], [4.14, 5.14]]
    pq3_res2 = vqc.get_gradients(param_val, ham, param_group_total=2, diff_method=DiffMethod.ADJOINT_DIFF)
    print('pq3_res2:', pq3_res2)
    print('pq3_res2.data():', pq3_res2.data())  # Returns a two-dimensional array as a 2-layer list, storing the gradient values corresponding to param_group_total sets of θ values
    print()
 
def fun3(vqc, ham):
    param_val = [2.14, 3.14]
    pq3_res3 = vqc.get_gradients_and_expectation(param_val, ham, diff_method=DiffMethod.ADJOINT_DIFF)
    print('pq3_res3:', pq3_res3)
    print('pq3_res3.data():', pq3_res3.data())  # Returns the result as a tuple. The first element of the tuple is the Hamiltonian expectation value. The second element is a one-dimensional array represented as a list, storing the gradient values corresponding to all element values of θ.
    print('pq3_res3.gradients():', pq3_res3.gradients())  # Returns a one-dimensional array as a list, storing the gradient values corresponding to all elements of θ
    print('pq3_res3.expectation_val():', pq3_res3.expectation_val())  # Returns the Hamiltonian expectation value
    print()
 
def fun4(vqc, ham):
    param_val = [2.14, 3.14, 4.14, 5.14]  # Or [[2.14, 3.14], [4.14, 5.14]]
    pq3_res4 = vqc.get_gradients_and_expectation(param_val, ham, param_group_total=2, diff_method=DiffMethod.ADJOINT_DIFF)
    print('pq3_res4:', pq3_res4)
    print('pq3_res4.data():', pq3_res4.data())  # Returns the result as a list of tuples. Stores the gradient values and Hamiltonian expectation values corresponding to param_group_total sets of θ values. The first element of the tuple is the Hamiltonian expectation value. The second element is a one-dimensional array represented as a list, storing the gradient values corresponding to all element values of θ.
    print()
 
vqc = get_vqc()  # Prepare the variational quantum circuit U(θ)
ham = get_hamiltonian()  # Prepare the Hamiltonian operator. It is recommended not to use 'H' as the variable name to avoid naming conflicts with the H gate.
fun1(vqc, ham)  # Demonstrate interface 1
fun2(vqc, ham)  # Demonstrate interface 2
fun3(vqc, ham)  # Demonstrate interface 3
fun4(vqc, ham)  # Demonstrate interface 4

Output result of the example code

pq3_res1: {gradient(double):{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}}
pq3_res1.gradients(): [0.011090474368968659, 23.39317090007428]
 
pq3_res2: (gradient(double)):[{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932},{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}]
pq3_res2.data(): [[0.011090474368968659, 23.39317090007428], [0.011090474368968659, 23.39317090007428]]
 
pq3_res3: (gradient and expectation){"expectation":-0.017333,"gradients":{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}}
pq3_res3.data(): (-0.01733304686759475, [0.011090474368968659, 23.39317090007428])
pq3_res3.gradients(): [0.011090474368968659, 23.39317090007428]
pq3_res3.expectation_val(): -0.01733304686759475
 
pq3_res4: ((gradient and expectation)):[{"expectation":-0.017333,"gradients":{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}},{"expectation":-0.017333,"gradients":{Parameter.at([0]):0.0110905,Parameter.at([1]):23.3932}}]
pq3_res4.data(): [(-0.01733304686759475, [0.011090474368968659, 23.39317090007428]), (-0.01733304686759475, [0.011090474368968659, 23.39317090007428])]

The application in VQA

An QAOA Example

The combinatorial optimization problem addressed by this example code is the Maximum Cut problem[5]: Given a graph with N vertices, label each vertex with 0 or 1 such that the number of edge cuts is maximized (an edge cut refers to an edge where the labels of its two vertices are different).

Example Code

from pyqpanda3.hamiltonian import PauliOperator,Hamiltonian
from pyqpanda3.vqcircuit import VQCircuit, VQCResult,ParamExpression,DiffMethod
from pyqpanda3.core import H, RZ, T, RX, RY,CNOT,S,X,I,QCircuit, QProg, CPUQVM
 
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
 
def generate_random_graph(n):
    g = nx.random_regular_graph(4, n)
    for u, v in g.edges:
        g[u][v]['weight'] = np.random.uniform(-1, 1)
        # g[u][v]['weight'] = 2
    return g
 
def test_qaoa():
    """
    <1>The core idea of QAOA is to prepare a parameterized quantum state on a quantum computer and then use a classical optimization algorithm to adjust these parameters so that the measurement result of the quantum state has a high probability of corresponding to an approximate optimal solution for the combinatorial optimization problem.
    <2>The parameterized quantum state can be obtained by applying a parameterized quantum circuit to an initial state.
    <3>The optimization problem addressed by this code is: Given a graph with N vertices, label each vertex with 0 or 1 such that the number of edge cuts is maximized (an edge cut refers to an edge where the labels of its two vertices are different).
    """
    def generate_ham(g):
        # Problem encoding: Encode the optimization problem as a Hamiltonian, whose ground state corresponds to the optimal solution of the problem.
        ham_list = []
        n = len(g.nodes)
        for u, v in g.edges:
            pauli_string = ['I'] * n
            pauli_string[u] = 'Z'
            pauli_string[v] = 'Z'
            ham_list.append((''.join(pauli_string), list(range(n)), g.edges[u, v].get('weight', -1)))
        return Hamiltonian(ham_list)
    def generate_qaoa_circuit(g, layers):
        # Prepare parameterized quantum circuit
        n = len(g.nodes)
        cir = VQCircuit()
        cir.set_Param([layers, 2])
        for i in range(n):
            cir << H(i)
        for layer in range(layers):
            for edge in g.edges:
                q0, q1 = edge
                weight = g.edges[edge].get('weight', 1)
                cir << CNOT(q0, q1) << RZ(q1, -2 * cir.Param([layer, 0]) * weight) << CNOT(q0, q1)
            for q in g.nodes:
                cir << RX(q, 2 * cir.Param([layer, 1]))
        return cir
    def optimize_params(vqc, ham):
        # Parameter optimization: Obtain the optimal parameter values to determine the quantum circuit (used to determine the optimal quantum state)
        # x0 = np.random.random(layers * 2)
        x0 = np.random.random(vqc.mutable_parameter_total())
        def get_expectation_and_grad(params, vqc, ham):
            params = np.reshape(params, vqc.get_Param_dims())
            exp_and_grad = vqc.get_gradients_and_expectation(params, ham, diff_method=DiffMethod.ADJOINT_DIFF)
 
            return exp_and_grad.data()
            # return exp_and_grad.expectation_val(), exp_and_grad.gradients() # Equivalent to exp_and_grad.data()
 
        from scipy.optimize import minimize
        final_res = minimize(get_expectation_and_grad, x0, args=(vqc, ham), jac=True)
        """ Code explanation
        (1) Introduction to scipy.optimize.minimize
            ① Function signature
                scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
            ② Parameter description
                fun: The objective function to minimize. It should accept an array as input and return a scalar value.
                x0: Initial guess, an array representing the initial values of the optimization variables.
                args: Additional arguments passed to the objective function and gradient function, passed as a tuple.
                method: String identifier for the optimization algorithm. Default is 'BFGS', but other algorithms can be chosen, such as 'Nelder-Mead', 'Powell', 'CG', 'Newton-CG', 'L-BFGS-B', 'TNC', 'COBYLA', 'SLSQP', etc.
                jac: Gradient of the objective function. If jac is a boolean and True, it is assumed that fun returns a tuple containing the gradient. If jac is a callable object, it should return the gradient.
            ③ Return value
                scipy.optimize.minimize 
                <1> The return value is an OptimizeResult object, which contains detailed information about the optimization process and the final result.
                <2> Key attributes
                    1> x: Stores the optimized parameter values.
                    2> success: A boolean value, True indicates that the optimization was successful, False indicates failure.
                    3> status: An integer representing the termination status of the optimizer. Different optimization algorithms may have different status codes. 0 usually indicates success, and other values may indicate different failure reasons.
                    4> fun: The value of the objective function after optimization, i.e., fun(x).
                    5> message: A string describing the termination message of the optimizer.
                    6> nfev: Number of evaluations of the objective function.
                    7> nit: Number of iterations of the optimizer.
                    8> jac: Gradient value at the end of optimization (if provided or calculated).
                    9> hess_inv: Inverse of the Hessian matrix at the end of optimization (if provided or calculated).
        (2) final_res = minimize(get_expectation_and_grad, x0, args=(cir, ham), jac=True)
            get_expectation_and_grad: This function calculates the Hamiltonian expectation value (corresponding to the scalar value to be returned) and gradient value (corresponding to parameter jac=True) based on the input parameters (a one-dimensional array).
            x0: Initial value of the parameters, with the same size as the array required by get_expectation_and_grad (determined by the variational quantum circuit (corresponding to vqc in args=(vqc,ham)) used in the function get_expectation_and_grad).
            args=(vqc,ham): The input parameters of get_expectation_and_grad are the values of the mutable parameters, the variational quantum circuit, and the Hamiltonian operator, where vqc and ham correspond to the variational quantum circuit and Hamiltonian operator, respectively.
            jac=True: The function get_expectation_and_grad will return the gradient value.
        """
        return vqc(final_res.x.reshape((layers, 2))).at([0])
    def measure_and_sample(cir):
        # Measurement and sampling: Under the optimized parameters, measure the quantum state to obtain samples of classical bits, which correspond to the approximate solution of the problem.
        prog = QProg()
        prog <<cir
        machine = CPUQVM()
        machine.run(prog, shots=1000) # Sample 1000 times
        final_measure = machine.result().get_prob_dict() # Get measurement results
        return final_measure
    def post_process(measure_res):
        # Post-processing and visualization of results
        final_measure = sorted(measure_res.items(), key=lambda i: i[1], reverse=True)[:10]
        labels = dict(zip(sorted(g.nodes), [i for i in final_measure[0][0][::-1]]))
        nx.set_node_attributes(g, labels, 'label')
        # print(final_res)
        # print(final_measure)
        plt.figure(figsize=(8, 6))
        pos = nx.spring_layout(g, seed=42)  # Layout algorithm
        # Draw nodes and edges
        nx.draw_networkx_nodes(g, pos, node_color='lightblue', node_size=500)
        nx.draw_networkx_edges(g, pos, edge_color='gray', width=1.5)
 
        node_labels = nx.get_node_attributes(g, 'label')
        nx.draw_networkx_labels(g, pos, labels=node_labels, font_color='darkred', font_size=12)
        edge_labels = {k: round(v, 3) for k, v in nx.get_edge_attributes(g, 'weight').items()}
        nx.draw_networkx_edge_labels(g, pos, edge_labels=edge_labels, font_color='green')
        plt.axis('off')
        plt.show(block=True)
 
    n = 8
    layers = 3
    g = generate_random_graph(n)                # The optimization problem addressed by this code is: Given a graph with N vertices, label each vertex with 0 or 1 such that the number of edge cuts is maximized (an edge cut refers to an edge where the labels of its two vertices are different)
    ham = generate_ham(g)                       # (1) Problem encoding: Encode the optimization problem as a Hamiltonian, whose ground state corresponds to the optimal solution of the problem.
    vqc = generate_qaoa_circuit(g, layers)      # (2) Prepare parameterized quantum circuit
    circuit = optimize_params(vqc, ham)         # (3) Parameter optimization: Obtain the optimal parameter values to determine the quantum circuit (used to determine the optimal quantum state)
    measure_res = measure_and_sample(circuit)   # (4) Measurement and sampling: Under the optimized parameters, measure the quantum state to obtain samples of classical bits, which correspond to the approximate solution of the problem
    post_process(measure_res)                   # (5) Post-processing and visualization of results
 
if __name__ == '__main__':
    test_qaoa()

Output result of the example code

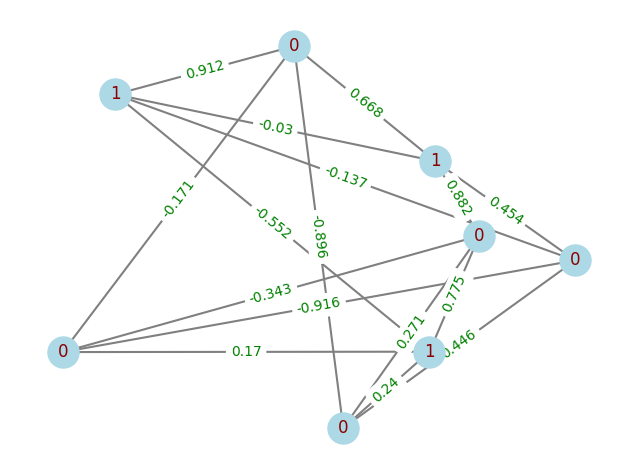
qaoa

Note: The topological structure of the graph in the above code is randomly generated, so the results of running the code may vary each time. The images shown above are only for demonstrating the effect of the program's execution.

References

[1] Cerezo M, Arrasmith A, Babbush R, et al. Variational quantum algorithms[J]. Nature Reviews Physics, 2021, 3(9): 625-644.

[2] Baydin A G, Pearlmutter B A, Radul A A, et al. Automatic differentiation in machine learning: a survey[J]. Journal of machine learning research, 2018, 18(153): 1-43.

[3] Jones T, Gacon J. Efficient calculation of gradients in classical simulations of variational quantum algorithms[J]. arXiv preprint arXiv:2009.02823, 2020.

[4] Luo X Z, Liu J G, Zhang P, et al. Yao. jl: Extensible, efficient framework for quantum algorithm design[J]. Quantum, 2020, 4: 341.

[5] Original Quantum. QAOA算法[EB/OL]. https://quantum-book-by-originq.readthedocs.io/en/latest/rst/4.5QAOA算法.html

Table of Contents

Basic Concepts

Variational Quantum Algorithm

Parameterized Quantum Circuit

Parameterized Quantum State

The Hamiltonian Expectation in Variational Quantum Algorithms

Gradient Computation in Variational Quantum Algorithms

Basic Usage Methods

General Usage Procedure

Prepare a Parameterized Quantum Circuit

Obtain The Parameterized Quantum State After Applying Given Parameter Values

Calculate The Hamiltonian Expectation Value

Calculate The Gradient Values

Other Usage Methods

Parameter θ In The Form Of A Matrix Or Tensor

Determination Of The Number Of Elements In The Parameter θ

Expression Evaluation

Other Interfaces For Gradient Calculation And Hamiltonian Expectation Value Calculation

The application in VQA

An QAOA Example

References